For every constraint handling method 100 optimization procedures were performed with random initial configurations. The proved optimal packing density is (5-sqrt(5))/3 ~ 0.921310674166737
Penalty function based on feasibility
I used the penalty function from this paper: An efficient constraint handling method for genetic algorithms
The closest the algorithm got to the optimum was 0.921310674166735 in 2 instances with the constraint violation of 1.110223024625157e-16. This is also the minimum constraint violation achieved in 100 runs. This same value of constraint violation had 53 other instances with mean 0.921310674166652 and variance 2.276453802275327e-25.
The overall mean density from the 100 runs was 0.8926 and variance 0.0061.
In 99 instances the output solution violated constrains. In these cases the mean of constraint violation was 0.002671273212076 and variance 1.732259359382852e-04.
Dynamic penalty
I’ve tested the dynamic penalty function from: A survey of constraint handling techniques used with evolutionary algorithms
In 100 experiments all of the output solution violated the constraints. the minimum constrain violation in these 100 instances was 0.8888 and mean constraint violation 1.5547. This is very bad.
An interesting observation is that when I replaced the values of the objective function with the maximum of feasible solutions (as in Penalty function based on feasibility) in the penalty function the algorithm suddenly performed very well.
Annealing penalty
Same case as with dynamic penalty.
Death penalty
Not really good. Gets stuck in configurations where it can’t find any feasible samples very quickly.
Repair
Very slow and not very precise due to the way the repairing is implemented. That is by multiplying the unit cell by a small constant c>1 until there is no overlap.
Augmented lagrangian method
I’ve implemented the augmented lagrangian method for the xNES from this paper: Augmented Lagrangian Genetic Algorithm for Structural Optimization
Same as in the case of dynamic penalties. All of the 100 experiments outpu solutions violated the constraints. The mean constraint violation was 1.0899 with variance 0.0020. Not useful at all.
Augmented lagrangian method with penalty function based on feasibility
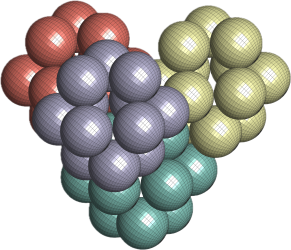
In 45 cases the algorithms output solution’s nonlinear constrains were distanced from zero less then 1.110223024625157e-16. Out of these 32 were unfeasible. From the feasible solutions the maximum density was 0.921310674166734 and the constraint violation of 0. Below is a picture of this solution.
The mean density of these 45 cases was 0.9205 and variance 2.0456e-05. Overall the mean density was 0.8777 and variance 0.0107. In 79 cases the constraints were violated. with mean constraint violation of 0.0017 and variance 6.7180e-05.