In my previous post on Ionic Molecular Crystallization, I sketched a geometric analysis of a two-dimensional ionic molecular framework, guided by charged particle interactions, symmetry, and regular polygon packings. Since our real interest lies in three-dimensional frameworks, I wondered how this idea would translate into three dimensions. While still theoretical, the model feels promising—and surprisingly beautiful.
To help me visualise the constructions, I discovered a wonderful CAD modelling software, Shapr3D, which is both intuitive to use and very powerful. I had zero experience with CAD before, but within a few hours, I was able to build all kinds of three dimensional frameworks.
Let’s start with the simplest regular polyhedron—the regular tetrahedron—and build a periodic framework by connecting the vertices of tetrahedra, as shown in the picture below.

Unfortunately, regular tetrahedra are not space-filling. In fact, the densest known packing of tetrahedra is currently a dimer packing with ![]() space group symmetry and a density of
space group symmetry and a density of ![]() (Chen, E.R., Engel, M., & Glotzer, S.C. Dense Crystalline Dimer Packings of Regular Tetrahedra. Discrete Comput. Geom. 44, 253–280 (2010). https://doi.org/10.1007/s00454-010-9273-0). However, I suspect that this packing might turn out to be a
(Chen, E.R., Engel, M., & Glotzer, S.C. Dense Crystalline Dimer Packings of Regular Tetrahedra. Discrete Comput. Geom. 44, 253–280 (2010). https://doi.org/10.1007/s00454-010-9273-0). However, I suspect that this packing might turn out to be a ![]() or
or ![]() tetrahedra monomer packing.
tetrahedra monomer packing.
The question is: how many regular tetrahedra can share one vertex subject to crystallographic restrictions? The answer is eight, as shown in the image below. This is a simple consequence of the sphere kissing number being 12. It forms a uniform star polyhedron called an octahemioctahedron.

The next question is: what might a local cluster with low net electrostatic energy look like? Here is one such arrangement of blue (![]() ) and green (
) and green (![]() ) charged particles that satisfies this criterion under the Coulomb potential.
) charged particles that satisfies this criterion under the Coulomb potential.


Additionally, I used the GEOMAG construction toy to build a physical model of this configuration. The green bars represent the repulsive forces in the green anion octahedral configuration. The white bars represent the attractive forces between green anions and blue cations; however, this is not entirely correct. These should not be represented as rigid rods but as tendons that can change length.
Geometrically, the GEOMAG structure represents the 1-skeleton of a stellated octahedron. The projection of the two tetrahedra, which together form the stellated octahedron, becomes visible in the shadow cast by the setting sun.
We set the configuration such that the local cluster’s Coulomb energy—introduced in the Ionic Molecular Crystallisation—is zero.
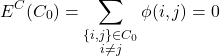
In terms of an optimisation problem, the configuration is a solution to the following:
![]()
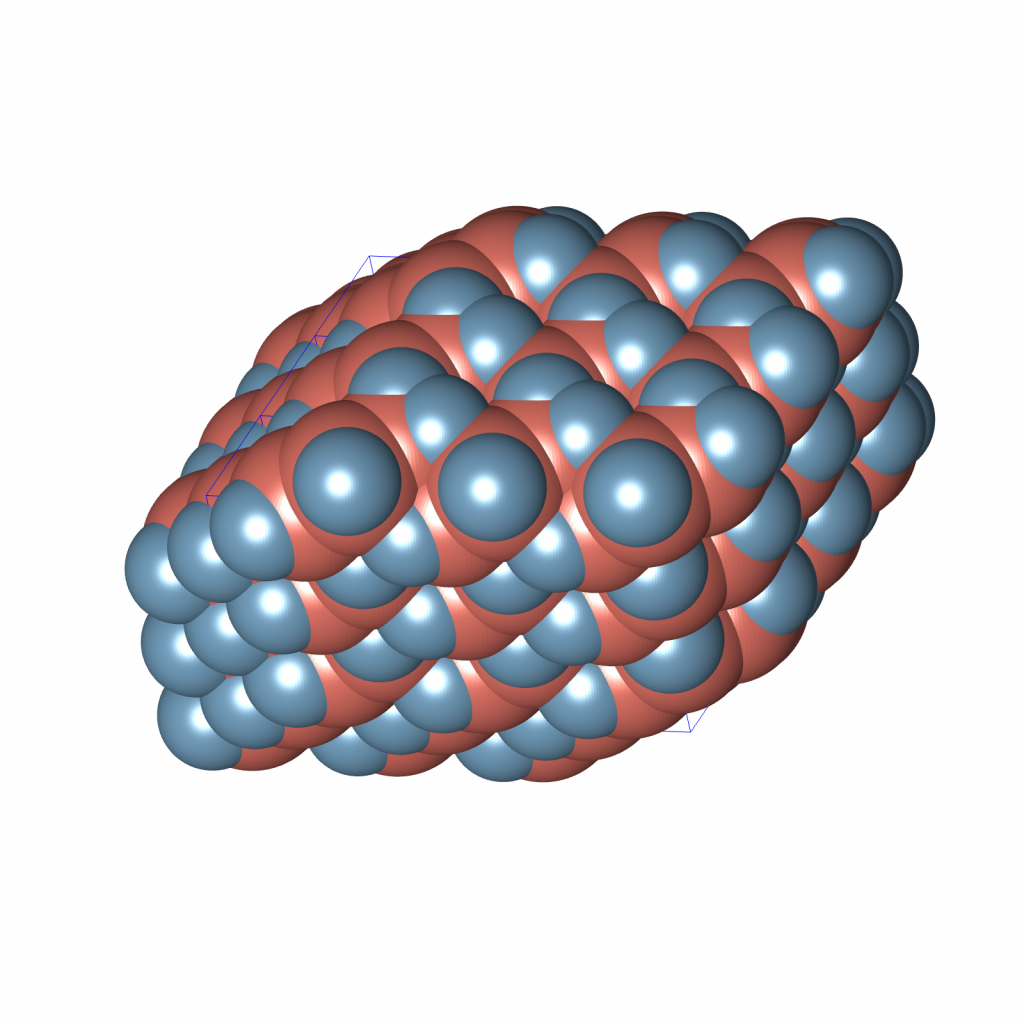
As in the two-dimensional case, the positively charged particles (blue) are located in the tetrahedral face-centred cubic (FCC) interstitial voids.

The local configuration of positively charged tetrahedral molecules and single-atom negatively charged molecules looks like this:
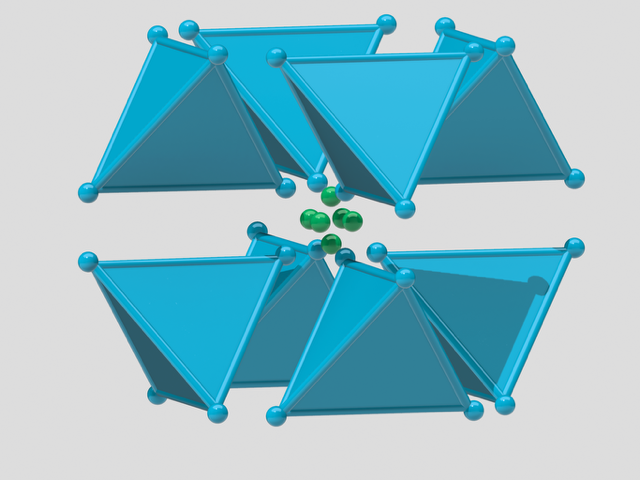
Once we assemble these octahemioctahedra, the resulting framework exhibits ![]() symmetry (space group 225)—the same as fluorite (
symmetry (space group 225)—the same as fluorite (![]() ). The similarity is not merely mathematical; chemically, the tetrahedral framework model could approximate a real organic fluorite structure, provided we can identify the appropriate molecular analogue.
). The similarity is not merely mathematical; chemically, the tetrahedral framework model could approximate a real organic fluorite structure, provided we can identify the appropriate molecular analogue.

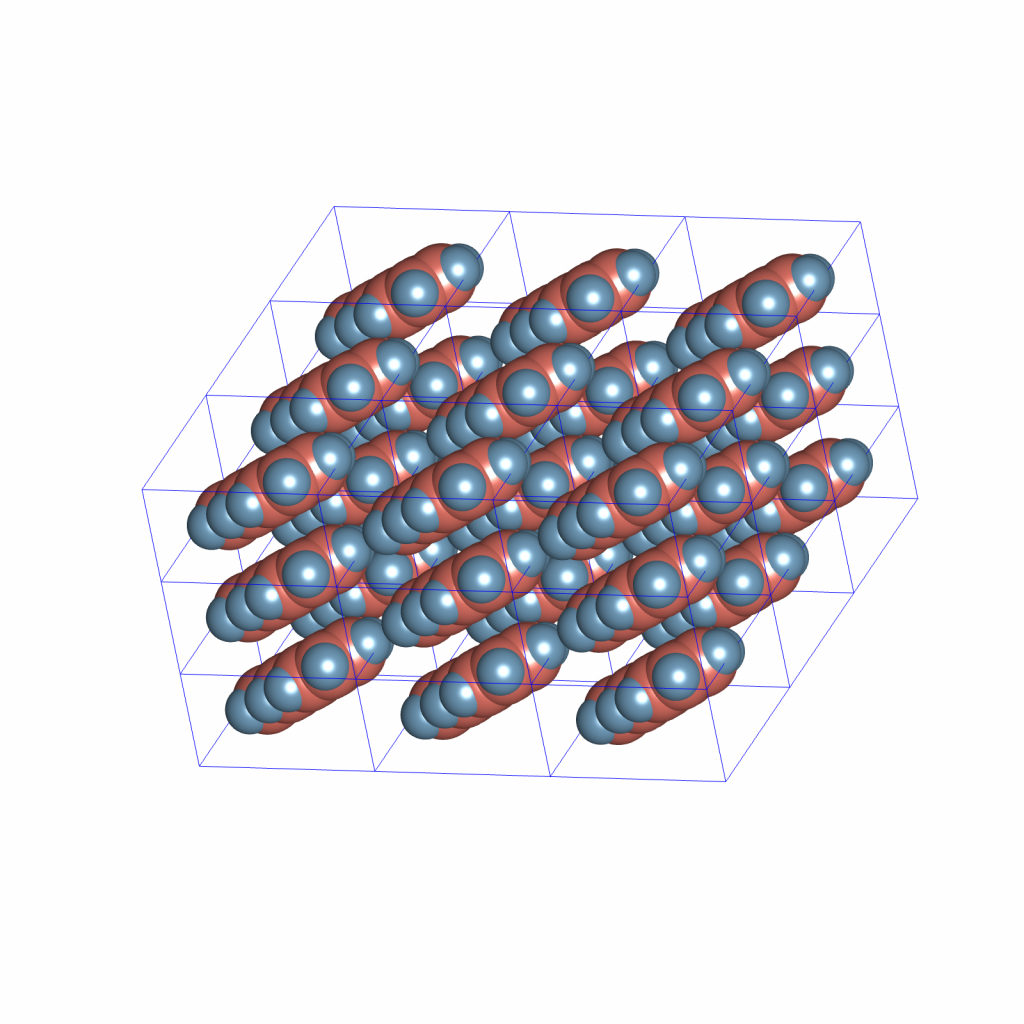
One can view this as the tetrahedral-octahedral honeycomb, where the octahedral building blocks have been removed. I positioned the camera to highlight the six-fold and four-fold roto-inversions of the framework.
Following the two-dimensional triangular tiling case, I constructed the following framework by removing tetrahedra from the ![]() framework while preserving crystallographic symmetry:
framework while preserving crystallographic symmetry:

The framework’s structure becomes clearer when in motion. See the animation below:
This is the three-dimensional equivalent of the lowest-density triangular configuration (Kagome lattice) from the Ionic Molecular Crystallisation post—the quarter cubic honeycomb. Its space group is ![]() (space group 227).
(space group 227).
As in the case of triangular tiling, there is a group-subgroup relationship between the tetrahedral-octahedral and the quarter cubic honeycombs via the space group ![]() (space group 224).
(space group 224). ![]() is the maximal index
is the maximal index ![]()
![]() -subgroup of
-subgroup of ![]() , and
, and ![]() is the maximal index
is the maximal index ![]()
![]() -subgroup of
-subgroup of ![]() . This should not come as a surprise given how the framework was constructed.
. This should not come as a surprise given how the framework was constructed.
If the observations from the two-dimensional framework analysis translate to three dimensions, this framework should represent a local Coulomb energy minimum, and a global minimum if the symmetries of the molecular system are constrained to the ![]() space group symmetry isomorphism class.
space group symmetry isomorphism class.
Similar to triangular frameworks, one can associate a sphere packing with the ![]() tetrahedral framework, and further with a regular
tetrahedral framework, and further with a regular ![]() -polytope, using these to enumerate local energy minima.
-polytope, using these to enumerate local energy minima.
This suggests a potential geometric design principle: Higher symmetry often corresponds to greater mechanical stability, whereas its sub-frameworks may offer larger pores or other advantageous properties at the expense of rigidity.
In other words, if our Coulomb cluster-tetrahedral structure minimises energy under ![]() symmetry, then the lower-symmetry frameworks derived from it (e.g.,
symmetry, then the lower-symmetry frameworks derived from it (e.g., ![]() ) may also represent local minima—stable enough to exist, but metastable within the full energy landscape.
) may also represent local minima—stable enough to exist, but metastable within the full energy landscape.
Moreover, we can define a generative method for exploring neighbourhoods of local energy optima by sampling an entire family of ionic molecular frameworks through the simple identification of symmetry-breaking subgroups of a highly symmetrical parent structure. That is, we begin with the framework exhibiting the highest symmetry and then systematically investigate its symmetry-reduced subframeworks.
Interestingly, some coarse-grained molecular simulations already approximate molecules as rigid polyhedra. Our goal is to create stable framework models with large cavities, which may serve as blueprints for the computational design of organic frameworks, applicable to areas such as atmospheric water harvesting and CO₂ capture.
In summary, referring back to previous posts (Chiral Interaction Ground States and Ionic Molecular Crystallisation), these configurations are all related through the face-centred cubic lattice packing of spheres, with a density of ![]() ,
,
and the following absolutely symmetric quadratic form:
![]()
courtesy of K. L. Fields (K. L. Fields, 1979. Stable, fragile, and absolutely symmetric quadratic forms. Mathematika, 26(1), 76–79).
This brings us full circle to the symmetries of FCC sphere packing explored in these blog posts:
![]()
![]()
Based on these, A. I. Kitaigorodsky (link to German Wikipedia page as no English version exists) formulated his Close Packing Principle:
“The mutual arrangement of the molecules in a crystal is always such that the ‘projections’ of one molecule fit into the ‘hollows’ of adjacent molecules.”
— From Molecular Crystals and Molecules by A. I. Kitaigorodsky
So, what’s next? I’m now looking into how kinematics of the cuboctahedron under space group symmetry constraints can help identify which polyhedral frameworks are mechanically stable—and which ones are just aesthetically pleasing. After my visit to ICERM and a conversation with Robert Connelly, I’m convinced that the mathematics of tensegrities is the key.




Postscript: I discovered that Shapr3D has a neat Augmented Reality feature. We had some fun with it in our office. Check out the photos below:


What Do Geodesic Polyhedra and X-ray Crystallography Have in Common?
During her visit to Liverpool, Zuzka—my fiancée Lina’s mom—gifted us these glass geodesic polyhedra. When sunlight shines through them, it scatters across our living room walls, creating miniature rainbows.

While preparing to travel to ICERM’s workshop, Matroids, Rigidity, and Algebraic Statistics, I noticed that the geodesic polyhedra formed a dilated triangular lattice pattern on the wall.
This is, in fact, the basic idea behind X-ray diffraction, discovered by Max von Laue in 1912. When electromagnetic waves-such as X-rays-pass through a crystal, the symmetrical arrangement of atoms causes the waves to diffract. When these waves hit an impenetrable surface, we can photograph the resulting wave interference pattern, composed of both constructive and destructive interactions.
One key challenge in X-ray crystallography is reconstructing a crystal’s atomic structure from its diffraction pattern—an example of an inverse problem. For instance, the mini-rainbow triangular lattice in the photo arises from the six-fold rotational symmetry of our two glass tetrahedral geodesic polyhedra.
One can perceive the situation at hand as a stereographic projection of a spherical model (as in Magnus Wenninger‘s book, Spherical Models) onto the two-dimensional plane, thereby relating the infinite triangular lattice to the “sphere of reflection”-i.e., Ewald’s sphere.
The idea of hanging transparent geodesic shapes in front of the window—creating rainbows across the room—came from Lina’s dad and my teacher, Oleg Šuk. He experimented with different materials, including an acrylic geodesic heart (with “acrylic” referring here to PMMA photonic crystal). I can’t help but wonder if the Šuk family is secretly guiding my work. See my previous posts, Chiral Interaction Energy Ground States and Yayoi Kusama’s Chandelier of Grief: Symmetry in Art and Science, for additional context.
Ionic Molecular Crystallization
A few months ago, I encountered an interesting problem related to molecular crystallization. Consider a two-dimensional system with two types of molecules: the first type consists of rigid triangles with positive charges localized at the vertices (shown as blue triangles in the image below), and the second type is a single-atom molecule with a negative charge (shown as a green dot).

Our key questions are:
- Does this molecular system crystallize in the thermodynamic limit?
- If so, what are the characteristics of its ground states?
Let’s assume the system’s intermolecular interactions follow a normalized Coulomb/electrostatic potential:
![]()
where ![]() and
and ![]() denote molecules of either type (green negative or blue positive triangular),
denote molecules of either type (green negative or blue positive triangular), ![]() is the Euclidean distance between charges
is the Euclidean distance between charges ![]() and
and ![]() . For green particles,
. For green particles, ![]() , while for vertices of blue triangles,
, while for vertices of blue triangles, ![]() . This creates attractive forces between opposite charges and repulsive forces between like charges, proportional to their relative distance.
. This creates attractive forces between opposite charges and repulsive forces between like charges, proportional to their relative distance.
The intermolecular energy is defined as the sum of all pairwise interactions ![]() between molecules
between molecules ![]() and
and ![]() :
:
![]()
This quantity generally lacks an infimum, so we need additional constraints.
We aim to find a sequence of molecular configurations ![]() where the following limit converges to a constant:
where the following limit converges to a constant:
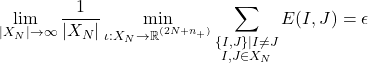
Here, ![]() represents a collection of
represents a collection of ![]() molecules of both types (
molecules of both types (![]() ).
).
Let’s focus on local clusters, as shown below:
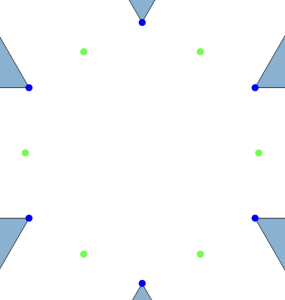
For any ![]() where
where ![]() , an alternating configuration of charges in a local cluster can found for any
, an alternating configuration of charges in a local cluster can found for any ![]() . Moreover, due to the rigidity of triangular molecules and the form of the potential
. Moreover, due to the rigidity of triangular molecules and the form of the potential ![]() , the maximal cluster contains
, the maximal cluster contains ![]() charges.
charges.
In our example cluster, ![]() , we set the energy to:
, we set the energy to:
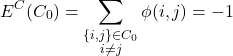
for demonstration purposes.
Alternatively, the cluster configuration can be expressed in the form of the optimization problem:
![]()
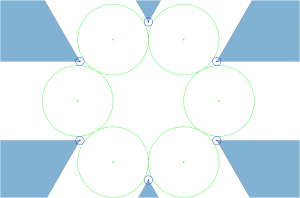
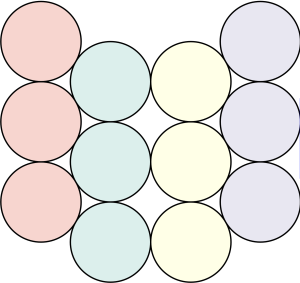
In the ![]() configuration, the blue positive charges occupy the interstitial voids of the hexagonal close-packed arrangement of negative green charges:
configuration, the blue positive charges occupy the interstitial voids of the hexagonal close-packed arrangement of negative green charges:
Following these local optimizations, we define a quantity we call the energy per cluster as:
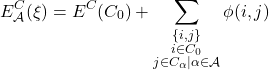
where ![]() is an index set . Minimizing
is an index set . Minimizing ![]() for such a cluster collection becomes a well-defined problem:
for such a cluster collection becomes a well-defined problem:
![]()
For cardinality ![]() , the solution is illustrated below.
, the solution is illustrated below.

Note that the interaction potential ![]() respects molecular memberships—for
respects molecular memberships—for ![]() and
and ![]() , we require
, we require ![]() .
.
We can expand ![]() to
to ![]() :
:
or any ![]() .
.
What we did is that we transformed the problem of finding molecular system minimizers into finding minimizers of a single-particle system with potential ![]() for
for ![]() , and we already know that the global minimizer is a dilated, translated, or rotated version of the triangular lattice.
, and we already know that the global minimizer is a dilated, translated, or rotated version of the triangular lattice.
Geometrically, this transformation effectively contracts local clusters into single points, resulting in a regular triangular tiling:
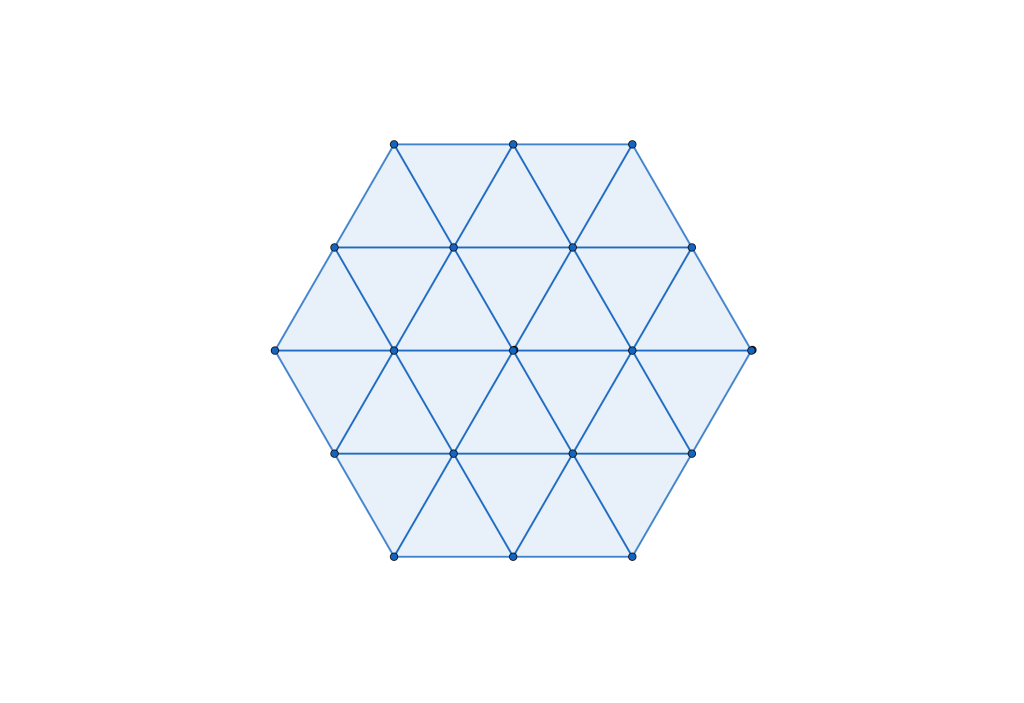

Having resolved the crystallization question, let’s examine the ground states’ characteristics, starting with a natural question: Are there other possible crystal phases? (From the materials science perspective, this question is important because of Crystal polymorphism)
On one side we can view our ground state configuration as a triangular tiling because of the rigidity of the blue molecules. On the other side, because of the way we have reframed the intermolecular interactions in terms of pairwise cluster interactions we may view the ground state configuration as the triangular lattice. The connecting point of these two views are the Archimedean circle packings and their associated semi-regular tessellations.
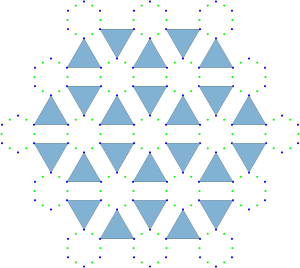
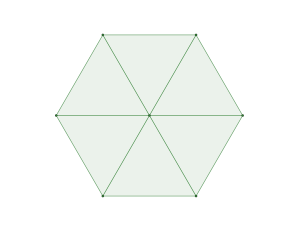
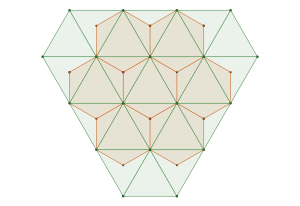
The densest packing of regular triangles is the ![]() configuration with a density of
configuration with a density of ![]() . It is, in fact, a tiling of triangles as shown below.
. It is, in fact, a tiling of triangles as shown below.
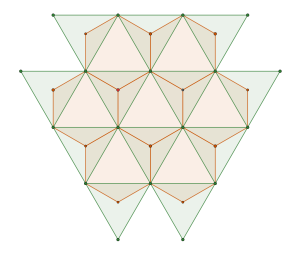
The maximal non-isomorphic subgroup of ![]() is the
is the ![]() plane group. The densest packing of regular triangles when the packing configurations are restricted to the
plane group. The densest packing of regular triangles when the packing configurations are restricted to the ![]() isomorphism class has a density of
isomorphism class has a density of ![]() and is shown in the image below.
and is shown in the image below.
This is, in fact, a consequence of removing one of the mirror symmetries from the ![]() plane group.
plane group.
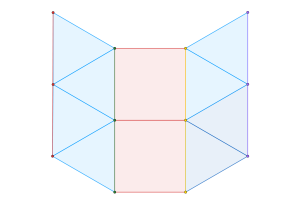
Another way to get here is to look at ![]() , the Archimedean framework
, the Archimedean framework
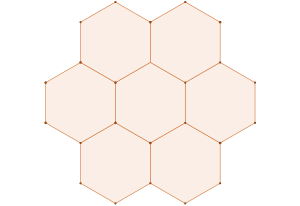
associated with the ![]() disc packing with packing density of
disc packing with packing density of ![]()
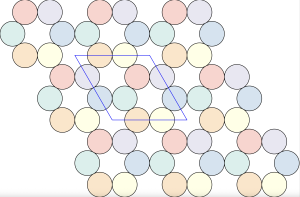
, and the Archimedean framework associated with the hexagonal close packed configuration of disc with density ![]()
and its associated Archimedean framework
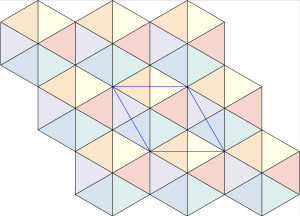
By interlacing the hexagonal and triangular frameworks
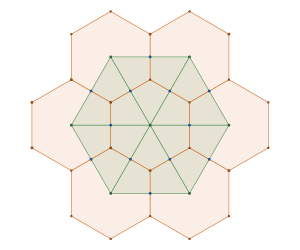
we construct new framework. The common (blue) intersection point of the hexagona and triangular frameworks in fact define a triangular sub-tiling
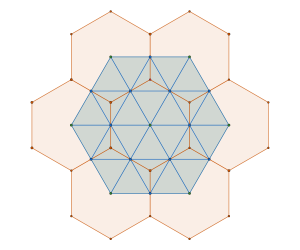
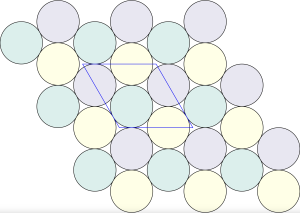
and the p![]() is constructed by removing triangle tiles containing a vertex at its center of mass
is constructed by removing triangle tiles containing a vertex at its center of mass
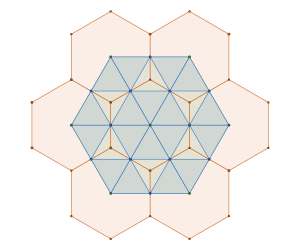

Alternatively we can create a complementary triangle packing with density of ![]() by removing tiles not containing an interior vertex
by removing tiles not containing an interior vertex
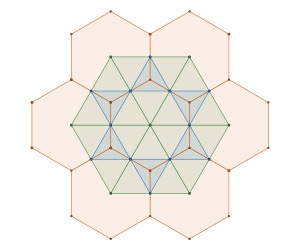

The resulting structure is sometimes referred to as the Kagome Lattice, although it is not a lattice per se.
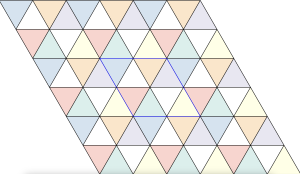
Starting from the ![]() triangle packing which is in fact a tiling
triangle packing which is in fact a tiling

and decomposing it into two complementary packings with ![]() symmetry with density of
symmetry with density of ![]()


This should come as no surprise since ![]() is the a maximal t-subgroup of
is the a maximal t-subgroup of ![]() of index 3.
of index 3.
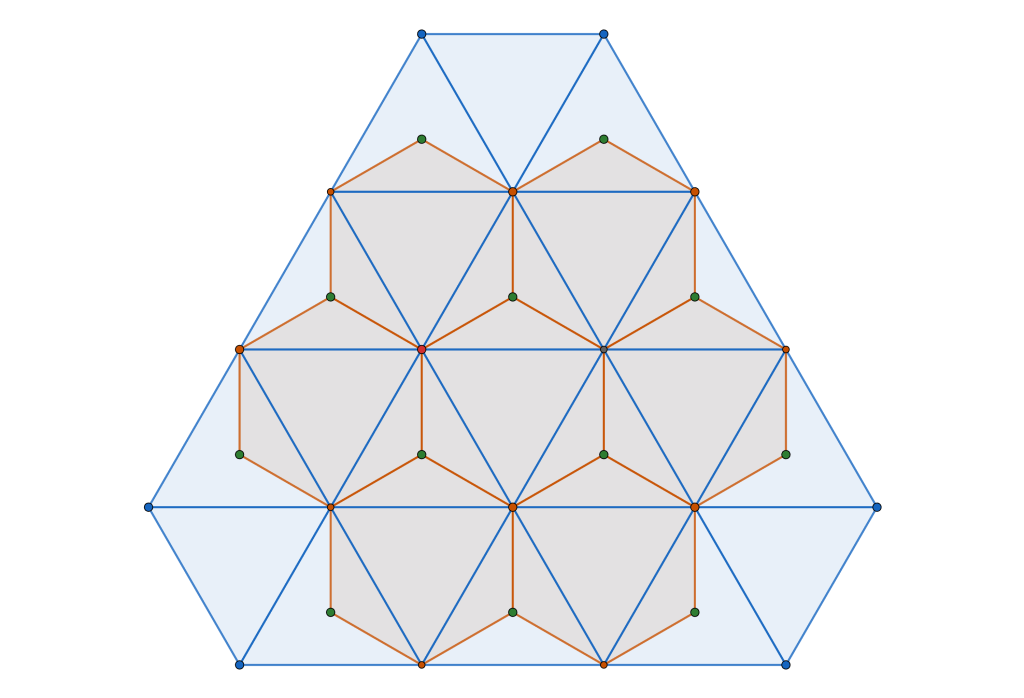
To demonstrate this point, we start again from the ![]() disc packing framework
disc packing framework
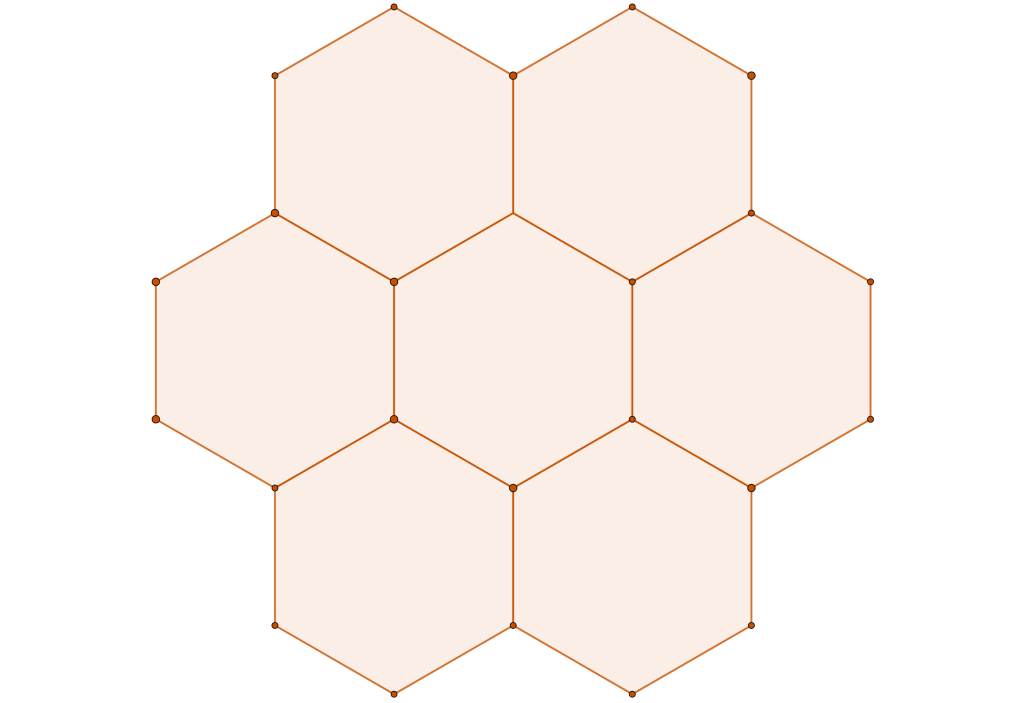
and interlace it with the triangular framework associated with ![]() packing of discs
packing of discs
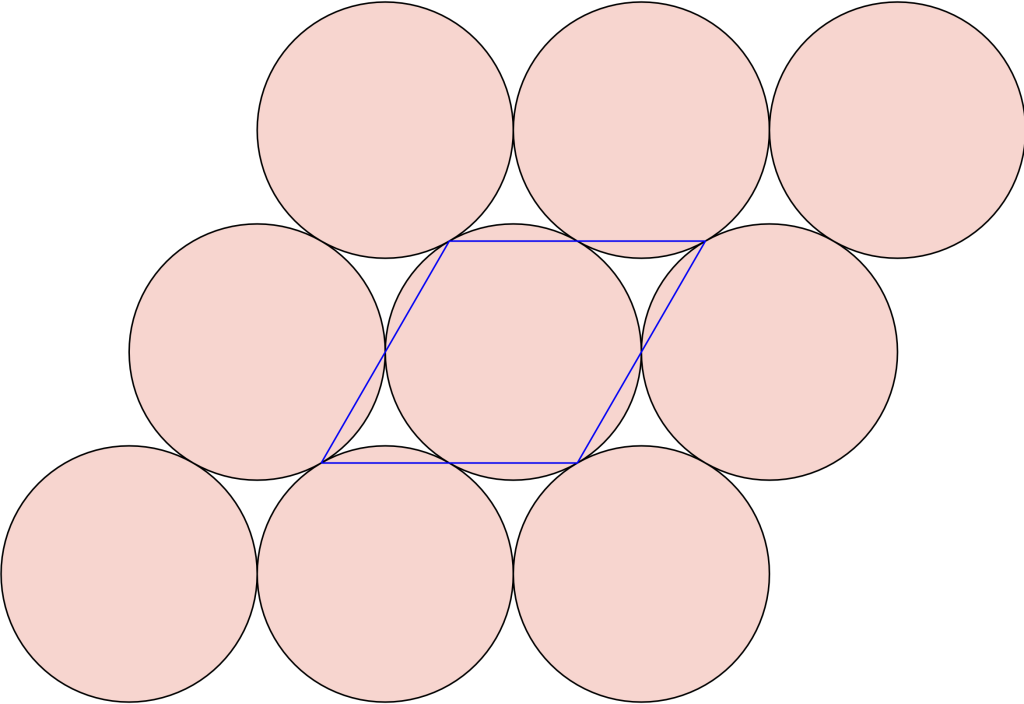
in such a way that disc centers are are subsets of the hexagon vertices
and we remove one ![]() symmetry from the tiling, the one not having a hexagon vertex at its center.
symmetry from the tiling, the one not having a hexagon vertex at its center.
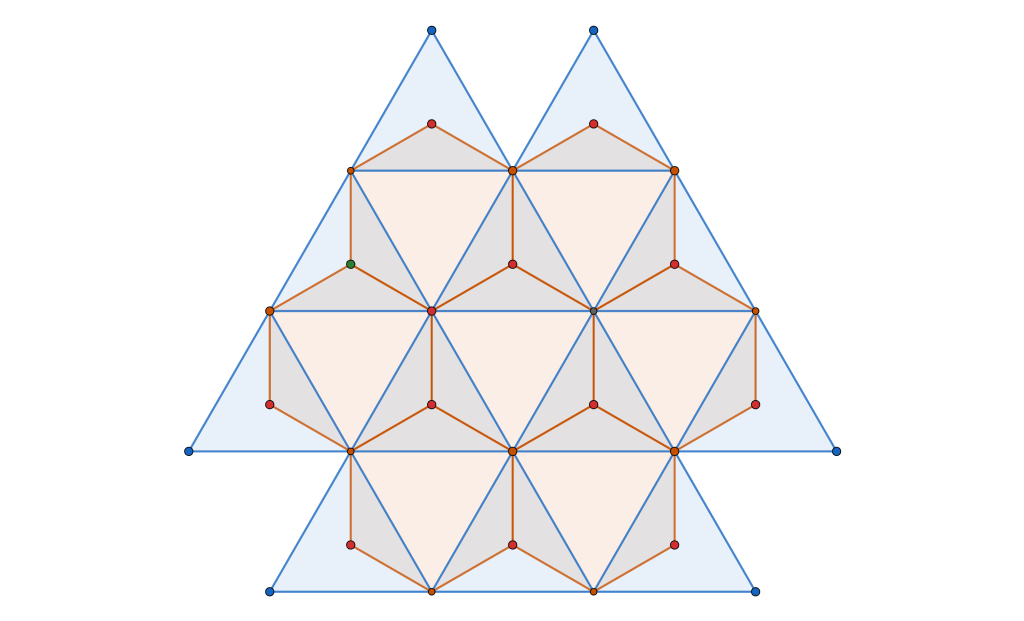
In fact, there are two possibilities to achieve the same result by using the triangle tiling above and rotating it by ![]() with respect to zero (center of the middle pentagon).
with respect to zero (center of the middle pentagon).
and do exactly the same thing as previously to get the second ![]() triangle tiling
triangle tiling
Combining these two triangle packings,
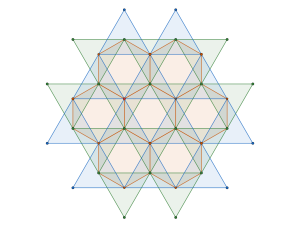
the ![]() symmetry of
symmetry of ![]() should be clearly visible.
should be clearly visible.
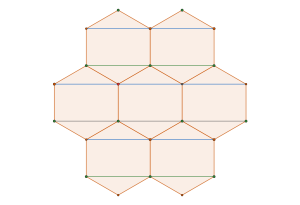
This tiling is a isomorphic to the one of the Archimedean (semi-regular vertex transitive) tilings associated with the densest ![]() packing of discs with density of
packing of discs with density of ![]()
with it’s ![]() semi-regular tiling
semi-regular tiling
These constructions are nothing new. For a comprehensive treatment of regular and semi-regular tilings, I recommend Regular Polytopes by H. S. M. Coxeter, first published in 1947. (Coxeter was the geometer who inspired M. C. Escher, which resulted in the Circle Limit I–IV series.)
Returning to our original problem of characterizing and enumerating possible Coulomb potential ground states of our molecular system, all these triangle packings represent viable local energy minima. This conclusion follows from our transformation of the intermolecular interactions into a nearly spherically symmetric “energy per cluster” potential, which preserves all symmetries of the hexagonal close-packing configuration of discs: p2, p2gg, pg, p3, and p1, as well as the rigidity of the triangular molecule.
We have classified the packings by associating each configuration with Archimedean disc packings and tessellations. The global energy minimizer corresponds to the triangular tiling and lattice, as demonstrated by Theil in “A Proof of Crystallization in Two Dimensions” (Commun. Math. Phys. 262, 209–236, 2006). https://doi.org/10.1007/s00220-005-1458-7. Since all our configurations are subsets of the triangular tessellation relative to some tiling symmetry subgroup, they are energy minimizers within their respective symmetry groups. (See Bétermin, L. “Effect of Periodic Arrays of Defects on Lattice Energy Minimizers,” Ann. Henri Poincaré 22, 2995–3023, 2021. https://doi.org/10.1007/s00023-021-01045-0.)
A property of Archimedean tessellations is that they are vertex-transitive, meaning the same number, ![]() , of regular
, of regular ![]() -gons meet at each vertex. In triangular tessellations, six regular triangles (
-gons meet at each vertex. In triangular tessellations, six regular triangles (![]() -gons) meet at each vertex. For regular tessellations like the triangular one, this follows a simple equation:
-gons) meet at each vertex. For regular tessellations like the triangular one, this follows a simple equation:
![]()
This is only for one type of polygon, but we have more types. However, we can generalize this formula to n-types of polygons:
![]()
For example, the tessellation associated with the ![]() packing of discs shown above has every vertex surrounded by
packing of discs shown above has every vertex surrounded by ![]() regular
regular ![]() -gons (triangles) and
-gons (triangles) and ![]() regular
regular ![]() -gons (squares).
-gons (squares).
Ultimately, the equation above is simply a disguised form of the Euler characteristic for plane-connected graphs induced by the vertex figure of a semi-regular tessellation.
What does this mean in the context of our molecular system?
- The vertex figure of each ground state is determined by the leading contributions to its total energy.
- In training Graph neural networks for Machine-learned interatomic potentials, learning these interactions alone suffices for ground state prediction in such molecular systems, significantly improving computational efficiency.
-
Combined with the Crystallographic restriction theorem, this formula allows us to explore possible ground state configurations based on molecular shape. In a periodic configuration, for every
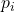 , there exists at least one
, there exists at least one 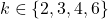 such that the expression
such that the expression 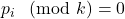 holds. Thus, for any such
holds. Thus, for any such 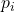 -gon shaped molecule, the vertex figure equation has only a finite number of integer solutions. Unfortunately, in cases like the pentagon, we might need to delve into the realm of aperiodic tilings.
-gon shaped molecule, the vertex figure equation has only a finite number of integer solutions. Unfortunately, in cases like the pentagon, we might need to delve into the realm of aperiodic tilings.
Chiral Interaction Energy Ground States
A few days ago, my beloved fiancé surprised me with a GEOMAG construction toy for my birthday. GEOMAG consists of small rods with embedded magnets and metallic spheres that can be assembled into various structures. It’s truly amazing—I had no idea something like this existed!
This toy can effectively model crystallography problems. For example, below is a geometric proof of the Crystallographic restriction theorem

It can also demonstrate structural rigidity problems, as shown in this framework
which becomes flexible after removing just one link.
The stable framework is actually the snub trihexagonal tiling – a regular tessellation associated with the p6 packing of discs.
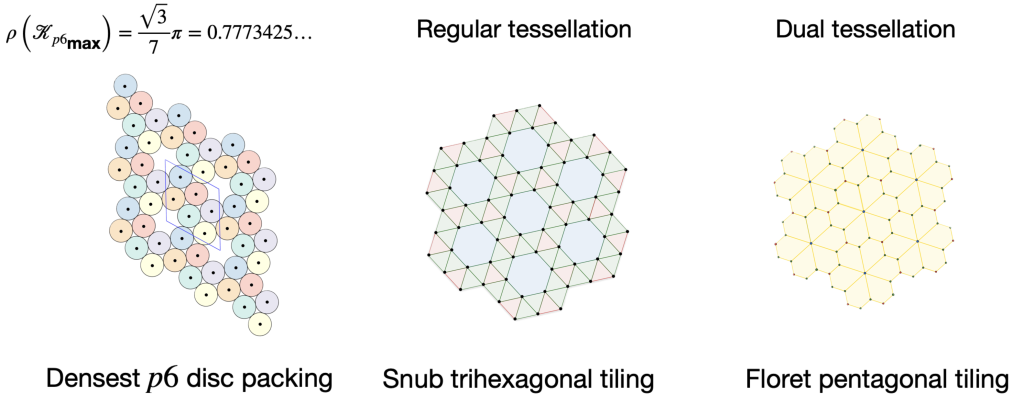
This framework is created by drawing links between the centers of touching disks. The tessellation on the right is called a floret pentagonal tiling. We can create this tiling from the p6 packing of hexagons by connecting each hexagon’s edge vertices to their nearest lattice points.

From the crystallographic perspective, the vertices of the dual tessellation lie in the
interstitial sites of the regular tessellation. Thus, the circles of the p6 packing are incircles of the pentagons in the floret pentagonal tiling and the hexagons in the hexagonal p6 packing.
This serves as a physical model of the Lennard-Jones system I described in my blog entry Lennard-Jones hexagonal molecular system. Through this model, I discovered that there are two chiral ground states connected by a continuous path in the configuration space.
Take a look at the animation below to see how it all works!
This is closely related to the vibrational part of lattice energy, degrees of freedom and structural stability of molecular crystals. Let’s have closer looks at this. Below is a visualization illustrating the transition between the chiral ground states of a 3-molecule cluster. Each molecule in the cluster contains six atoms. The intermolecular energy is given by the Lennard-Jones potential:
![Rendered by QuickLaTeX.com \begin{equation*} E_{LJ}=\sum_{\substack{\{I,J\} \\ I \cap J =0}} \sum_{\substack{(i,j ) \\ i \in I, j \in J}} \left[\left(\frac{1}{r_{(i,j)}}\right)^{12} - \left(\frac{1}{r_{(i,j)}}\right)^{6}\right] \end{equation*}](https://milotorda.net/wp-content/ql-cache/quicklatex.com-562681f5736399b7414a50ca69c95723_l3.png)
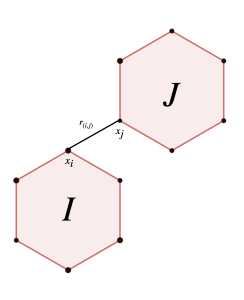
The chiral ground states are in clear energy potential wells and represent two different global solutions of the energy cluster ![]() minimization problem.
minimization problem.
From the GEOMAG model animation, one can imagine this cluster being held together only by the bonds between nearest neighbors. By allowing three of the total bonds to stretch, one introduces one degree of freedom into the otherwise rigid cluster, making it possible for the configuration to move to its neighboring potential well.
This however requires a short range interaction potential, since the pairwise interaction is computed among all atoms of different molecules not only the first neighbors. The Lennard-Jones potential is one such example where the leading contribution to the overall energy is the three atom cluster in the middle and the transition from one ground state to the other is animated as revolving around the centre of mass of this cluster.
It is also by this Lennard-Jones potential property that the ground state of this two-dimensional molecular system coincides with the densest ![]() packing of discs. This means that there are also two chiral densest
packing of discs. This means that there are also two chiral densest ![]() packings of all
packings of all ![]() -gons with six-fold rotational symmetry. This observation connects directly to my earlier work on plane group packings during my PhD, as it shows an aspect these packings I overlooked. The results of this study are published in our Densest plane group packings of regular polygons manuscript.
-gons with six-fold rotational symmetry. This observation connects directly to my earlier work on plane group packings during my PhD, as it shows an aspect these packings I overlooked. The results of this study are published in our Densest plane group packings of regular polygons manuscript.
Moreover, this explains the crystal defects in the Lennard-Jones hexagonal molecular system. Since mirror symmetry is not permitted in this two-dimensional system, we observe incompatible local ground state patches.
I was wondering if a real material with this crystal structure exists. In fact, it does, and it was published only a few years ago. See the image and reference below.


Rusek, M., Kwaśna, K., Budzianowski, A., & Katrusiak, A. (2019). Fluorine··· fluorine interactions in a high-pressure layered phase of perfluorobenzene. The Journal of Physical Chemistry C, 124(1), 99-106.
The above is a space-filling visualization of this high-pressure phase of perfluorobenzene, which is in excellent agreement with our highly simplified model. The sphere radii are set to the van der Waals radii. The left image shows one layer, while the right image displays the same layer with the carbons removed. The space group of this crystal is C2/c. C2/c symmetry consists of a two-fold rotational symmetry (here, within one layer of perfluorobenzene) and a perpendicular mirror symmetry. This effectively means that the layers alternate as two chiral two-dimensional ground states, interchanging chirality layer by layer.

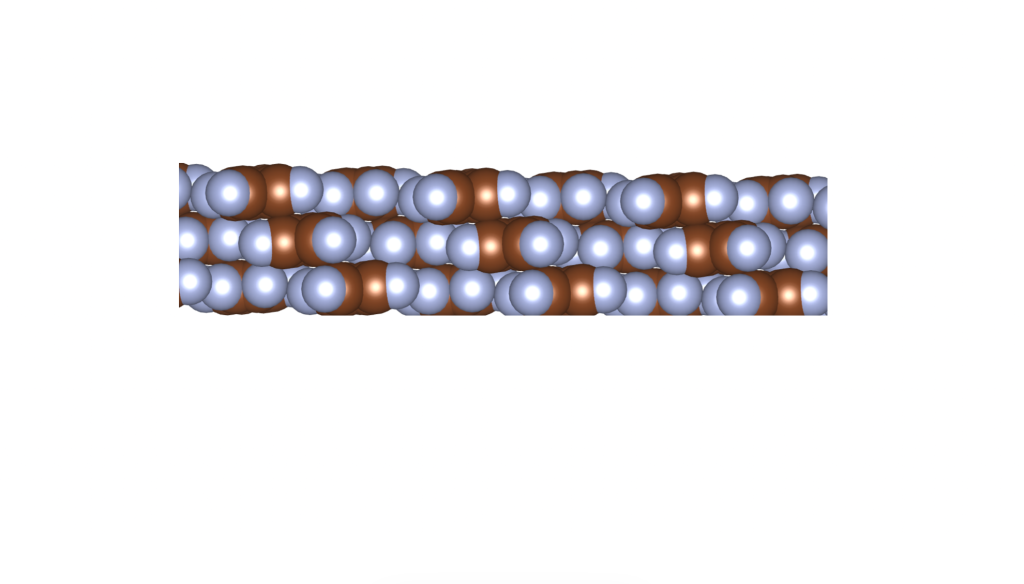
S – enantiomer

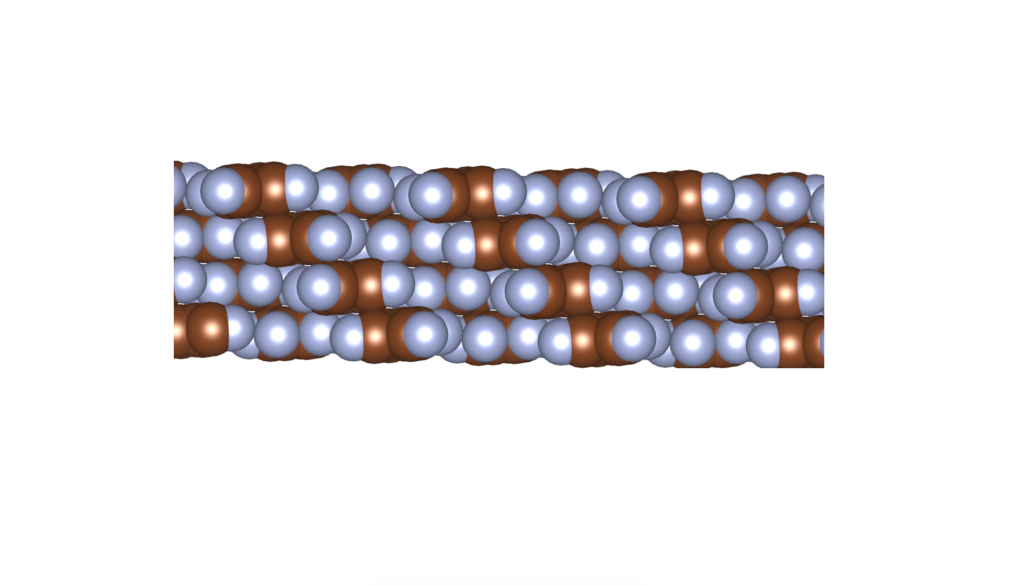
R – enantiomer

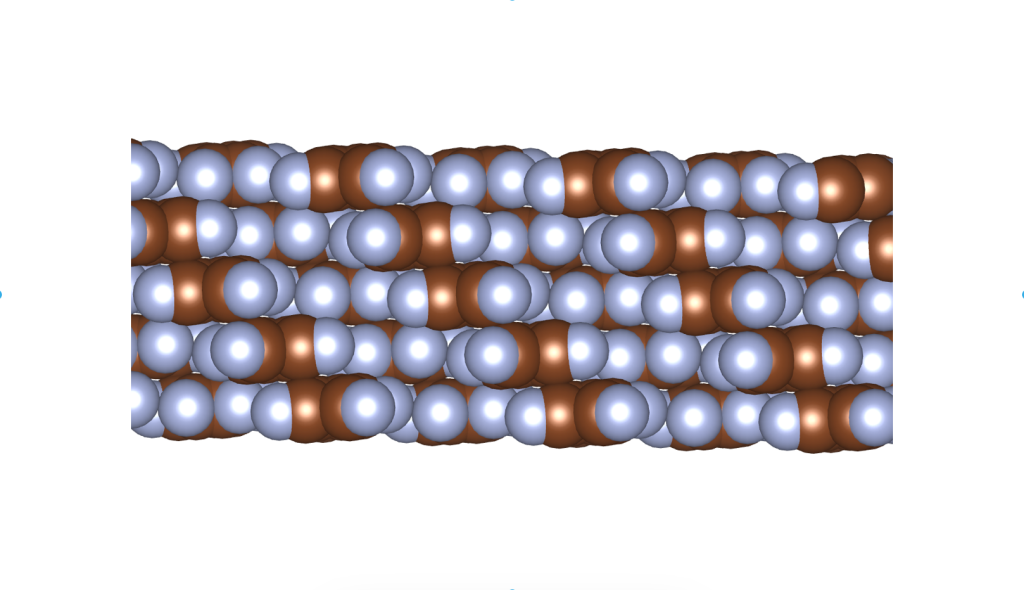
S – enantiomer
Why is this important beyond just creating appealing pictures and animations? One reason is that it can significantly reduce computational time complexity by eliminating unnecessary calculations in
Crystal Structure Prediction (CSP). For example, if we know beforehand that our target compound satisfies a few assumptions, the degrees of freedom to explore can be reduced to a maximum of 12, sometimes even less, as demonstrated in our Close-Packing approach to CSP (Alternatively, we can think of the hard sphere model as a pairwise interaction potential. However, in this blog, we are considering soft core interactions).
And we know time is money, as illustrated by the recent developments around the DeepSeek model and its ensemble learning approach to large language model training. The concept of ensemble here mirrors the
Thermodynamic ensemble that Gibbs introduced in 1902.
This also shows how chemistry can inspire the development of novel machine learning algorithms beyond Machine-learned interatomic potentials.
LRC Symposium Supplementary Materials
Ellsworth Kelly’s Yellow Curve: Axiomatic Art
Below is a photo I took at the exhibition of works by Ellsworth Kelly at the Louis Vuitton Foundation, which I visited on my way back from the CaLISTA Workshop on Geometry-Informed Machine Learning at Mines Paris.
He truly distilled art to its essentials—I’m sure Euclid would have approved.

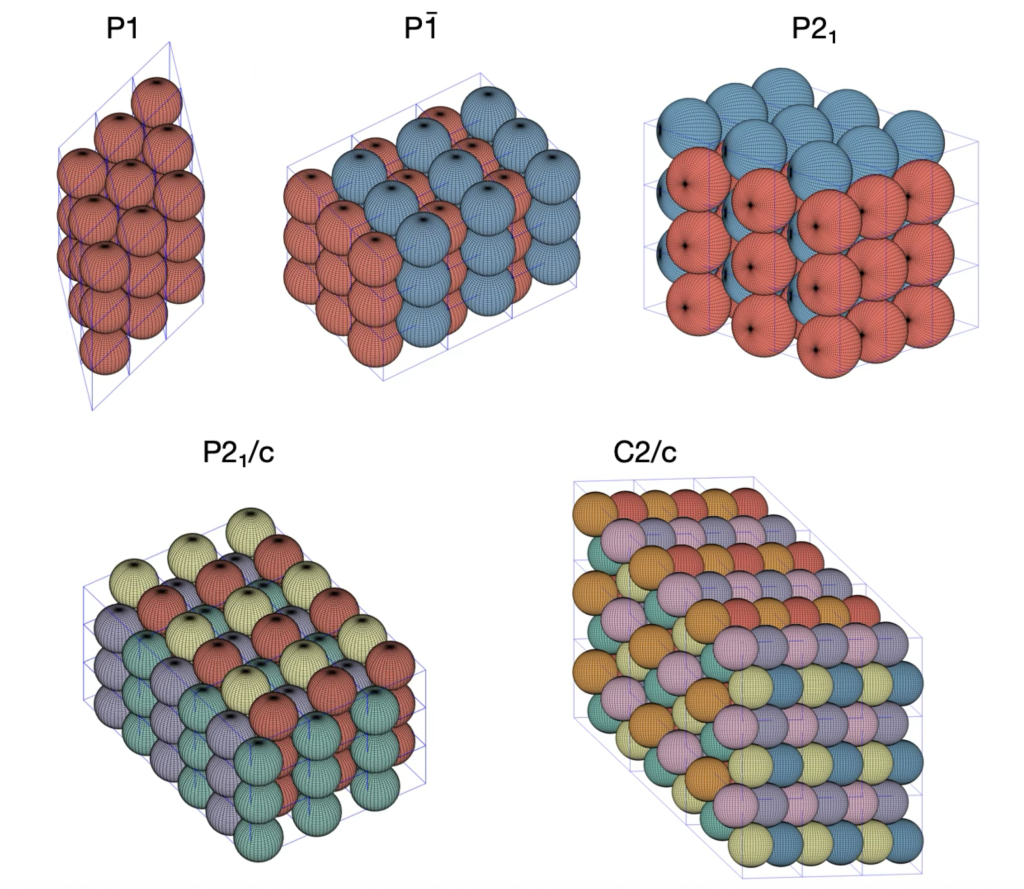
Sphere packings continued – space groups 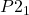 and
and 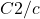
In this post, we’re diving back into the world of sphere packings, focusing on the space groups ![]() and
and ![]() . Feel free to check out an earlier discussion on Densest P1, P-1 and P21/c packings of spheres. Both of these groups reach the packing density of
. Feel free to check out an earlier discussion on Densest P1, P-1 and P21/c packings of spheres. Both of these groups reach the packing density of ![]() .
.
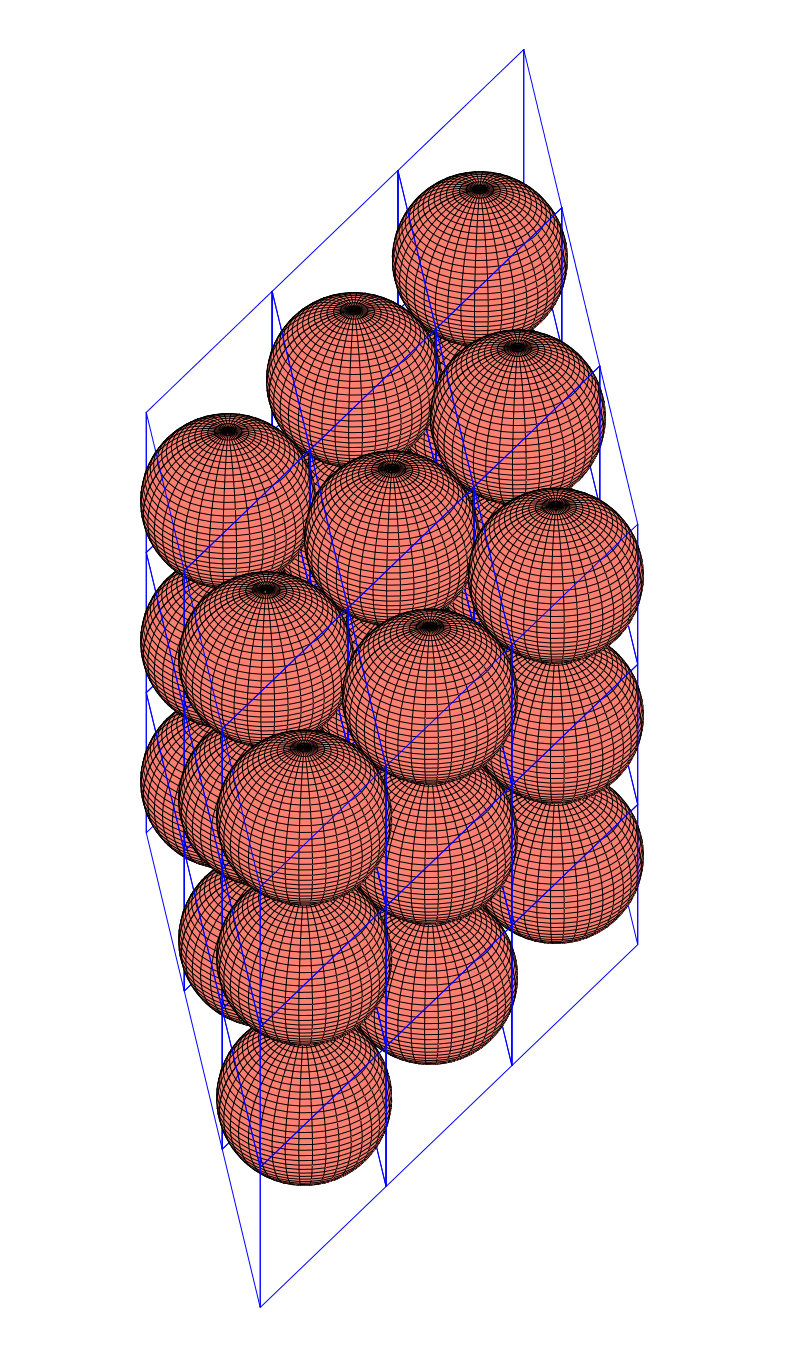
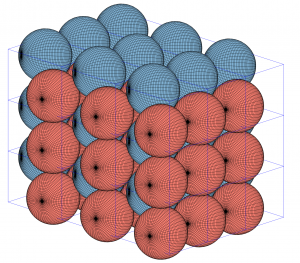
The densest ![]() packing almost identical to the
packing almost identical to the ![]() group. Even though they belong to different crystal systems—triclinic for
group. Even though they belong to different crystal systems—triclinic for ![]() and monoclinic for
and monoclinic for ![]() —they share the same unit cell parameters:
—they share the same unit cell parameters: ![]() ,
, ![]() , and
, and ![]() . Here’s a snapshot of what this packing looks like:
. Here’s a snapshot of what this packing looks like:
Next up is the ![]() space group, which also falls under the monoclinic category. This group is a bit more complex, with eight symmetry operations. Its densest packing has unit cell parameters of
space group, which also falls under the monoclinic category. This group is a bit more complex, with eight symmetry operations. Its densest packing has unit cell parameters of ![]() ,
, ![]() , and
, and ![]() . Check out the illustration below of the densest packing configuration:
. Check out the illustration below of the densest packing configuration:

So far, we’ve seen that the optimal packing density for the space groups ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() matches the general optimal sphere packing density. This isn’t too surprising since these groups are all related to the Hexagonal Closed Packed structure, via group – subgroup relations. Interestingly, these space groups are among the top ten of the most frequently occurring in the Cambridge Structural Database, making up 74% of its entries.
matches the general optimal sphere packing density. This isn’t too surprising since these groups are all related to the Hexagonal Closed Packed structure, via group – subgroup relations. Interestingly, these space groups are among the top ten of the most frequently occurring in the Cambridge Structural Database, making up 74% of its entries.
Yayoi Kusama’s Chandelier of Grief: Symmetry in Art and Science

This photo captures my fiancé Lina and myself at Yayoi Kusama’s “Infinity Mirror Rooms” exhibit at Tate Modern in London, taken in March 2024. The installation, called “Chandelier of Grief,” uses mirrors and light to explore ideas about symmetry.
The centrepiece of the artwork is a chandelier surrounded by six mirrors arranged in a regular hexagonal prism. This creates an interesting visual effect—an infinite lattice of chandeliers extending in all directions, with each reflected chandelier appearing at the centre of symmetry within this lattice.
What we’re experiencing is a visual representation of a hexagonal lattice, one of the five two-dimensional Bravais lattices. Mathematically, it represents a discrete group of isometries in two-dimensional Euclidean space. The point group of this hexagonal lattice is isomorphic to the dihedral group ![]() , highlighting its sixfold rotational symmetry and mirror reflection properties.
, highlighting its sixfold rotational symmetry and mirror reflection properties.
Physically, the hexagonal lattice emerges as the ground state configuration for systems of particles interacting via certain potentials, such as the Lennard-Jones potential, in the thermodynamic limit. Moreover, the hexagonal lattice is realised in materials like graphene, where carbon atoms arrange themselves in this highly symmetric pattern, leading to its unique properties.
Kusama’s installation is not only aesthetically pleasing but also serves as a visual representation of abstract concepts in mathematics and physics. The infinite reflections illustrate how artistic expression can intersect with scientific principles, making complex ideas accessible and engaging to a wider audience.
Exercise in Monte-Carlo packing density computation.
I needed a way to calculate the packing densities of structures modeled using the van der Waals sphere model, generated through CSP and DFT computations. Specifically, for periodic configurations, this comes down to computing:: ![]() . Here,
. Here, ![]() represents the volume of the unit cell
represents the volume of the unit cell ![]() , and
, and ![]() is the volume of the subset of
is the volume of the subset of ![]() occupied by the van der Waals spheres denoted as
occupied by the van der Waals spheres denoted as ![]() .
.
Calculating the volume of ![]() is is straightforward; it’s simply the determinant of the unit cell’s generators:
is is straightforward; it’s simply the determinant of the unit cell’s generators: ![]() . However, analytically computing the volume of
. However, analytically computing the volume of ![]() involves solving numerous intricate integrals of intersections of spheres with various radii, making it cumbersome.
involves solving numerous intricate integrals of intersections of spheres with various radii, making it cumbersome.
Let’s try to do this the Monte-Carlo way, instead. The volume of ![]() can be expressed as an integral over the unit cell
can be expressed as an integral over the unit cell ![]() , i.e.
, i.e.
![]()
Here, ![]() is the natural volume form on
is the natural volume form on ![]() . Since this integral is zero everywhere except in the unit cell, it can be redefined as an integral of the indicator function over the unit cell:
. Since this integral is zero everywhere except in the unit cell, it can be redefined as an integral of the indicator function over the unit cell:
![]()
By changing coordinates to an integral over the unit cube ![]() , we get:
, we get:
![]()
Plugging this into the density equation yields:
![]()
Considering ![]() as a uniform random vector on the unit cube, this integral represents the expected value of the indicator function with respect to the
as a uniform random vector on the unit cube, this integral represents the expected value of the indicator function with respect to the ![]() -variate uniform distribution. This, in turn, equals the probability of
-variate uniform distribution. This, in turn, equals the probability of ![]() lying in the collection of the van der Waals spheres
lying in the collection of the van der Waals spheres ![]() , scaled by the inverse of the unit cell:
, scaled by the inverse of the unit cell:
![]()
This means that the crystal’s density can be estimated by sampling ![]() , counting how many fall inside
, counting how many fall inside ![]() , and dividing by
, and dividing by ![]() :
:
![]()
Now, say I want to determine the density of this ![]() anthracene structure
anthracene structure
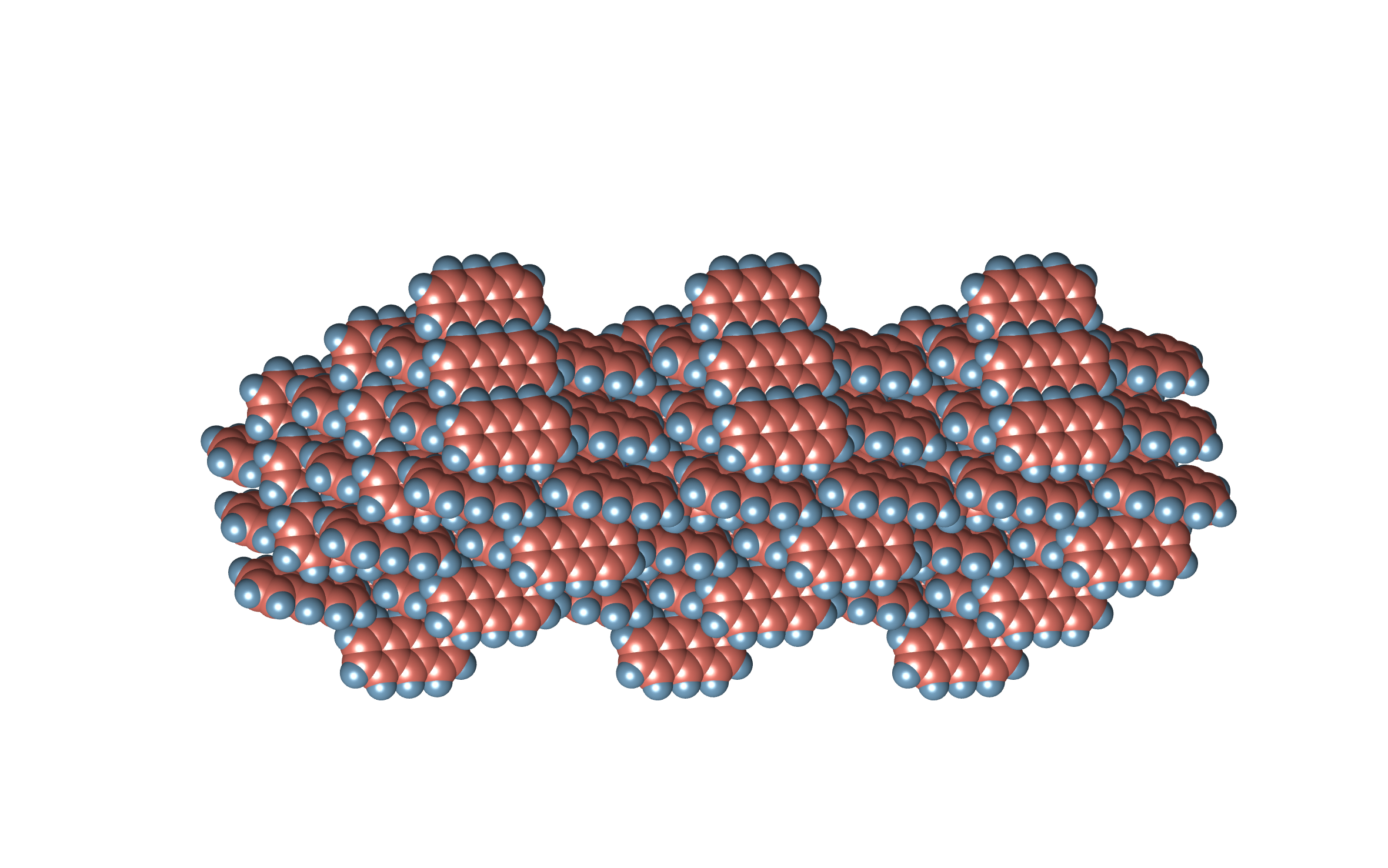
Equivalently, I can sample uniformly from the parallelepiped defined by the unit cell, e.g. ![]() realisations,
realisations,

and count how many fall inside at least one of the van der Waals spheres

which is ![]() . Therefore, the density estimate is
. Therefore, the density estimate is ![]() .
.
But how accurate is this estimate? Or even better, how large does ![]() need to be so that
need to be so that ![]() , where
, where ![]() is some constant?
is some constant?
To answer this, consider each ![]() as a Bernoulli trial. Then
as a Bernoulli trial. Then ![]() is a binomially distributed random variable with the expected value
is a binomially distributed random variable with the expected value ![]() and variance
and variance ![]() . According to the central limit theorem, the random variable
. According to the central limit theorem, the random variable ![]() converges in distribution to a normally distributed random variable with a mean of
converges in distribution to a normally distributed random variable with a mean of ![]() and a variance of
and a variance of ![]() . Therefore, I can request
. Therefore, I can request ![]() being in the interval
being in the interval ![]() , and I want the size of this interval to be less than some constant with probability
, and I want the size of this interval to be less than some constant with probability ![]() :
:
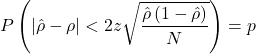
where ![]() is the
is the ![]() quantile of the standard normal distribution.
quantile of the standard normal distribution.
For the ![]() anthracene structure mentioned earlier, to achieve
anthracene structure mentioned earlier, to achieve ![]() with probability
with probability ![]() , I need
, I need ![]() . The density estimate in this case is then:
. The density estimate in this case is then:
![]()
As a point of comparison, CCDC’s Mercury reports the packing coefficient of this structure as ![]() .
Closing note: This method could also be used to quantify uncertainty about the true packing during ETRPA‘s optimization run in the tradition of Sequential analysis.
.
Closing note: This method could also be used to quantify uncertainty about the true packing during ETRPA‘s optimization run in the tradition of Sequential analysis.
Repairing Unfeasible Solutions in ETRPA.
The ETRPA is designed to optimize a multi-objective function by:
1. Maximizing packing density.
2. Minimizing overlap between shapes in a configuration.
This is achieved through the use of a penalty function, which generally works quite effectively. However, there are some downsides to this approach. Many generated samples are flagged as unfeasible, leading to inefficiency. Additionally, some potentially good configurations with minimal overlaps are discarded. A more effective approach would involve mapping unfeasible solutions to feasible ones, essentially repairing the overlaps.
I’ve designed a relatively straightforward method to accomplish this almost analytically. It boils down to finding roots of a second-order polynomial, which is essentially a high school algebra problem. Admittedly, you’ll need to solve quite a few of these second-order polynomials, but they are relatively easy to handle.
So, with this approach, you can now map a configuration with overlap/s
Now, a couple of new issues have cropped up. First, there are some seriously bad solutions that are being sampled. For example, consider this one:
This is not helpful at all. Second, the parameters of this configuration are way above the optimisation boundaries that were used to create all configurations. As a result, it falls outside the configuration space where my search is taking place.
To address this issue, after repairing the configuration, I conduct a check to determine if the repaired configuration falls within my optimization boundaries. Any configurations that fall outside of these bounds are labeled as unfeasible solutions.
It might seems this puts me back in the same situation of multi-objective optimization, but that’s not the case. In my scenario, the Euclidean gradient at time ![]() takes this form:
takes this form:
![]() .
.
Here, ![]() represents the mean of all samples in the current batch, and I only consider the configurations without overlap or the repaired ones that lie within the optimization boundaries for
represents the mean of all samples in the current batch, and I only consider the configurations without overlap or the repaired ones that lie within the optimization boundaries for ![]() . This effectively means I’ve eliminated the need for the penalty function and am optimizing only based on the objective function given by the packing density.
. This effectively means I’ve eliminated the need for the penalty function and am optimizing only based on the objective function given by the packing density.
This is a promising, but it does introduce another problem. When I repair some of the unfeasible configurations, I end up making slight alterations to the underlying probability distribution, shifting it slightly from ![]()
The issue here is that if I were to compute the Natural gradient as I used to, I’d obtain 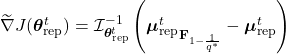 in the tangent space
in the tangent space ![]() of the statistical manifold, where everything is unfolding, but what I actually need is
of the statistical manifold, where everything is unfolding, but what I actually need is ![]() in the tangent space at the point
in the tangent space at the point ![]() .
.
Fortunately, the statistical manifold of the exponential family is a flat Riemannian manifold. So, first, I move from ![]() to
to ![]() using this vector
using this vector ![]() (where
(where ![]() corresponds to the dual Legendre parametrization of
corresponds to the dual Legendre parametrization of ![]() , and
, and ![]() to
to ![]() ), and then I compute the natural gradient at the point
), and then I compute the natural gradient at the point ![]() .
.
In addition, to increase the competition within my packing population, I introduce a sort of tournament by retaining the N-best configurations I’ve found so far and incorporating them with the repaired configurations from the current generation. This leads to yet another slightly modified distribution, ![]()
and I have to perform the same Riemannian gymnastics once more. In the end, the approximation to the natural gradient at the point ![]() is as follows
is as follows
![]()
![]()
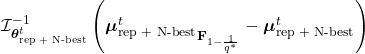
![]()
![]()
![]()
![]()
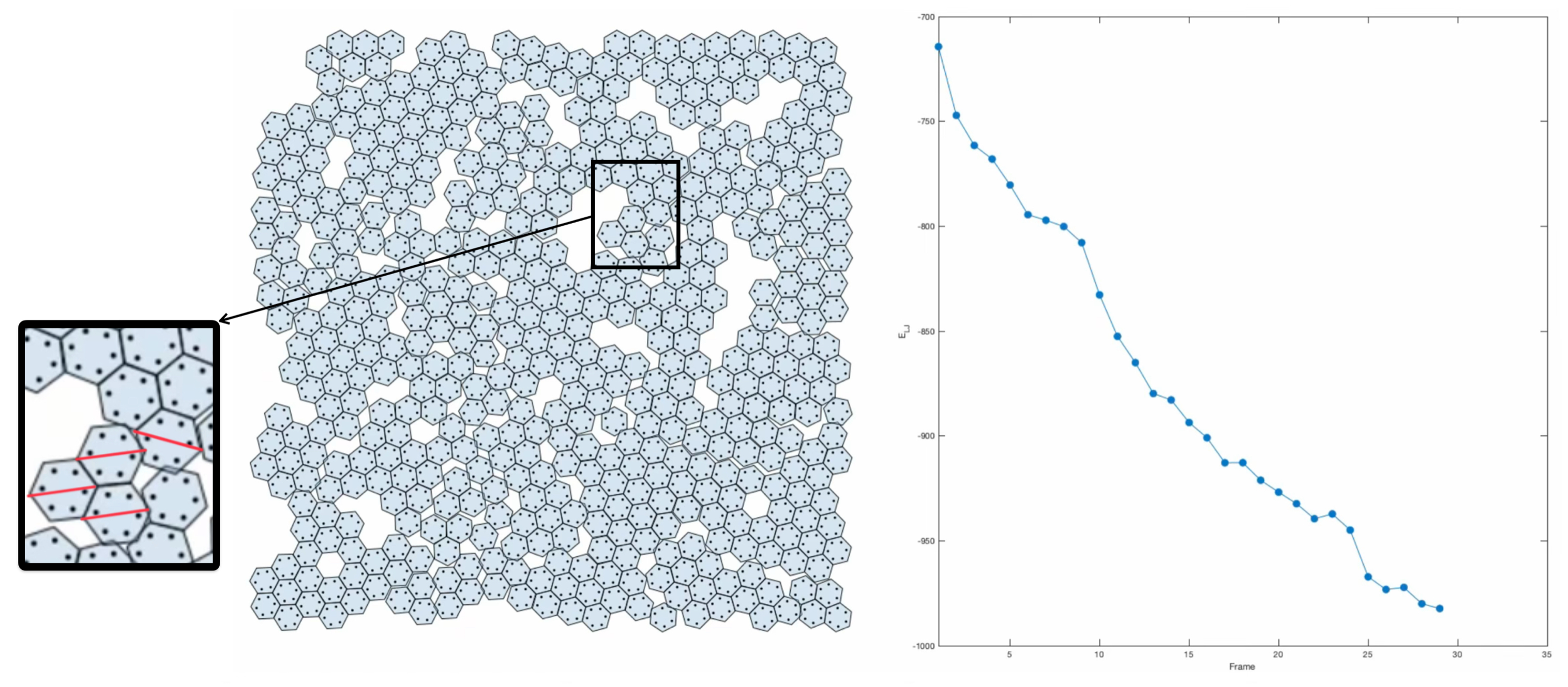
So far, experiments show that these modifications to the ETRPA are far more effective than the original ETRPA. Here’s a visualization from one of the test optimization runs:
In this particular run, the best packing I achieved attains the density of ![]() . Previously, reaching such a level of density required multiple rounds of the refinement process, each consisting of
. Previously, reaching such a level of density required multiple rounds of the refinement process, each consisting of ![]() iterations. Now, a single run with just
iterations. Now, a single run with just ![]() iterations is sufficient. It’s worth noting that even after only
iterations is sufficient. It’s worth noting that even after only ![]() iterations, the algorithm already reaches areas with densities exceeding
iterations, the algorithm already reaches areas with densities exceeding ![]() .
.
It’s important to mention that currently, I’ve only implemented the repair process for unfeasible configurations for the ![]() space group. However, similar repairs can be done for configurations in any space group. Furthermore, the algorithm’s convergence speed can be further enhanced by fine-tuning its hyperparameters. Perhaps it’s time to make use of the BARKLA cluster for the hyperparameter tuning.
space group. However, similar repairs can be done for configurations in any space group. Furthermore, the algorithm’s convergence speed can be further enhanced by fine-tuning its hyperparameters. Perhaps it’s time to make use of the BARKLA cluster for the hyperparameter tuning.