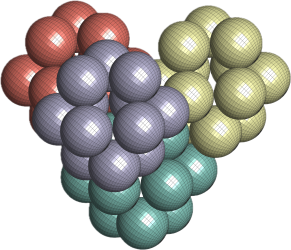
I applied the Entropic Trust Region Packing Algorithm to search for the densest lattice packing of tetrahedra. It turned out that the GPU implementation of the overlap constraint evaluation for space group packings of polyhedra was more complicated than I expected. The good news was that the optimization algorithm worked as thought.
The densest lattice packing of the regular tetrahedron is 
(https://www.ams.org/journals/bull/1970-76-01/S0002-9904-1970-12400-4/). This is the configuration the algorithm found. See the visualization of the output packing with density 
below.
