In this post, we’re diving back into the world of sphere packings, focusing on the space groups ![]() and
and ![]() . Feel free to check out an earlier discussion on Densest P1, P-1 and P21/c packings of spheres. Both of these groups reach the packing density of
. Feel free to check out an earlier discussion on Densest P1, P-1 and P21/c packings of spheres. Both of these groups reach the packing density of ![]() .
.
The densest ![]() packing almost identical to the
packing almost identical to the ![]() group. Even though they belong to different crystal systems—triclinic for
group. Even though they belong to different crystal systems—triclinic for ![]() and monoclinic for
and monoclinic for ![]() —they share the same unit cell parameters:
—they share the same unit cell parameters: ![]() ,
, ![]() , and
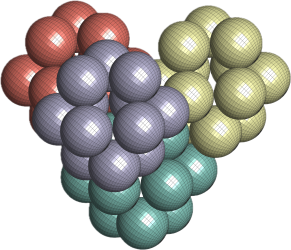
, and ![]() . Here’s a snapshot of what this packing looks like:
. Here’s a snapshot of what this packing looks like:
Next up is the ![]() space group, which also falls under the monoclinic category. This group is a bit more complex, with eight symmetry operations. Its densest packing has unit cell parameters of
space group, which also falls under the monoclinic category. This group is a bit more complex, with eight symmetry operations. Its densest packing has unit cell parameters of ![]() ,
, ![]() , and
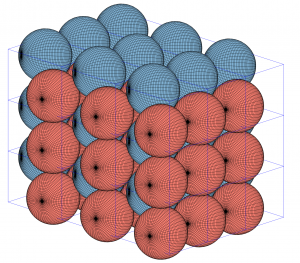
, and ![]() . Check out the illustration below of the densest packing configuration:
. Check out the illustration below of the densest packing configuration:

So far, we’ve seen that the optimal packing density for the space groups ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() matches the general optimal sphere packing density. This isn’t too surprising since these groups are all related to the Hexagonal Closed Packed structure, via group – subgroup relations. Interestingly, these space groups are among the top ten of the most frequently occurring in the Cambridge Structural Database, making up 74% of its entries.
matches the general optimal sphere packing density. This isn’t too surprising since these groups are all related to the Hexagonal Closed Packed structure, via group – subgroup relations. Interestingly, these space groups are among the top ten of the most frequently occurring in the Cambridge Structural Database, making up 74% of its entries.