16: MG, NARMA & TE cont.

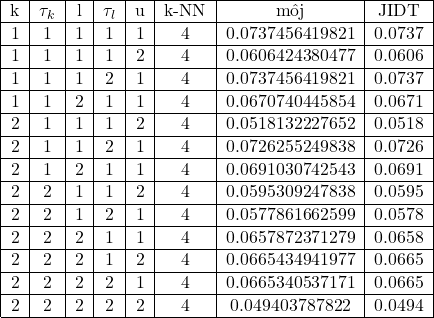
To isté čo pri #20 akurát s väčším rezervoárom + pridané korelácie medzi váhami rezervoárovej matice a transfer entropie tj. $\rho(w_{ij},TE_{X_{i}\rightarrow X_{j}})$

Parametre siete

	Standart	Normalized	Normalized & OG	Normalized & ON
Veľkosť rezervoiru	100	100	100	100
Train Length	1000	1000	1000	1000
Test length	1000	1000	1000	1000
Runs	10	10	10	10
W	N(0,1)	N(0,1)	N(0,1)	N(0,1)
Win MG	Unif[-0.5,0.5]	Unif[-0.5,0.5]	Unif[-0.5,0.5]	Unif[-0.5,0.5]
Win NARMA	Unif[0,0.4]	Unif[0,0.4]	Unif[0,0.4]	Unif[0,0.4]
Spectral radius	unscaled	0.9	0.9	0.9
Ortogonal	null	null	gradient descent	gradient descent
Wout training	pinv	pinv	pinv	pinv
Bias	false	false	false	false
Leaking rate	1	1	1	1
OG/ON iterations	0	0	30	30
OG/ON eta	0	0	0.03	0.070.9*t

Parametre estimátorov

	k_history	k_tau	l_history	l_tau	u	k
TE	1	1	1	1	1	4
AIS	1	1	null	null	null	4

Mackey – Glass

Mean reservoir

	Standart	Normalized	Normalized & OG	Normalized & ON
Mackey - Glass	0.0096	0.6245	0.6117	0.6351
NARMA	0.0093	0.0922	0.0801	0.0945

NRMSE

	Standart	Normalized	Normalized & OG	Normalized & ON
Mackey - Glass	1.1149	0.9577	0.6748	1.0472
NARMA	2.4119	0.8664	0.8338	0.8433

InputOutput TE

	Standart	Normalized	Normalized & OG	Normalized & ON
Mackey - Glass	-0.004	-0.0210	-0.0212	-0.0256
NARMA	-0.0013	0.3732	0.3743	0.3714

Mean reservoir-output TE

	Standart	Normalized	Normalized & OG	Normalized & ON
Mackey - Glass	-0.0001	0.3516	0.3601	0.3532
NARMA	-0.0006	0.0015	0.0014	0.0018

NARMA

AIS

Mean reservoir AIS

	Standart	Normalized	Normalized & OG	Normalized & ON
Mackey - Glass	0.0036	2.1694	2.1763	2.1910
NARMA	0.0023	0.1618	0.1675	0.1730

Zdrojaky:

NARMATEnormalizedOG.py

NARMATEnormalizedON.py

October 9, 2017October 22, 2017

MG, NARMA TE

Prvé runny použitia ESNtoolbox na analýzu ESN trénovanej na úlohu predikcie t+1 Mackey – Glass a NARMA.

Parametre siete

	Standart	Normalized	Normalized & Orto
Veľkosť rezervoiru	10	10	10
Train Length	1000	1000	1000
Test length	1000	1000	1000
Runs	10	10	10
W	Unif[0,1]	N(0,1)	N(0,1)
Win	Unif[0,1]	Unif[-0.1,0.1]	Unif[-0.1,0.1]
Spectral radius	unscaled	0.9	0.9
Ortonormal	null	null	QR
Wout training	pseudoinverse	pseudoinverse	pseudoinverse
Bias	false	false	false
Leaking rate	1	1	1

Parametre estimátorov

	k_history	k_tau	l_history	l_tau	u	k
TE	1	1	1	1	1	4
AIS	1	1	null	null	null	4

NRMSE

	Standart	Normalized	Normalized & Orto
Mackey - Glass	0.035	0.217	0.111
NARMA	0.878	0.898	0.966

TE

Mean reservoir

	Standart	Normalized	Normalized & Orto
Mackey - Glass	0.006	0.590	0.322
NARMA	-0.010	0.158	0.145

InputOutput TE

	Standart	Normalized	Normalized & Orto
Mackey - Glass	0.138	-0.003	0.321
NARMA	1.811	0.867	0.266

AIS

Mean-reservoir AIS

	Standart	Normalized	Normalized & Orto
Mackey - Glass	2.277	2.230	1.687
NARMA	0.392	0.354	0.110

Zdrojaky:

MGTE.py

MGTEnormalized.py

MGTEnormalizedORTO.py

NARMATE.py

NARMATEnormalized.py

NARMATEnormalizedORTO.py

Markov models from data by simple nonlinear time series predictors in delay embedding spaces

September 24, 2017October 22, 2017

Dal som dokopy knižnicu, ktorá zatiaľ implementuje:
KSG Transfer entropy estimator – TE (source, target, kHistory, kTau, lHistory, lTau, u, k)
KSG Active information storage estimator – AIS (target, kHistory, kTau, k)
ESN reservoir Memory capacity – MC(Win, W)

Zdrojaky:
ESNtoolbox.py

September 20, 2017October 22, 2017

Active Information Storage

Tak a je napisaný ďalší KSG estimator. Tentokrát AIS.

$\mathbf{A}_{X}^{(k)}(t)=\mathbf{I}(\mathbf{X}_{t-1}^{k}:X_{t})$

kde

$\mathbf{X}_{t-1}^{k}=({X}_{t-1},{X}_{t-1-\tau_{k}},{X}_{t-1-2\tau_{k}},...,,{X}_{t-1-(k-1)\tau_{k}})$

Zdrojaky:
AIS.py

September 18, 2017October 22, 2017

KSG TE continued 2

Podarilo sa urýchliť výpočet TE. k-d Tree je odpoveď.
Pri k=2, $\tau_{k}=1$ , l=2, $\tau_{l}=1$ , sample size N=645, 0.0115s vs. 155s predchádzajúca verzia.

Použité dáta:
SFI-heartRate_breathVol_bloodOx3.txt

Zdrojaky:
TE.py

September 17, 2017October 22, 2017

KSG TE continued

Rozšíril som KSG estimator TE na ľubovoľné nastavenia parametrov.

$\mathbf{T}_{Y\rightarrow X}^{(k,l)}(t)=\mathbf{I}(X_{t}:\mathbf{Y}_{t-u}^{l}\mid\mathbf{X}_{t-1}^{k})$

kde

$\mathbf{X}_{t-1}^{k}=({X}_{t-1},{X}_{t-1-\tau_{k}},{X}_{t-1-2\tau_{k}},...,,{X}_{t-1-(k-1)\tau_{k}})$

$\mathbf{Y}_{t-u}^{l}=({Y}_{t-u},{Y}_{t-u-\tau_{l}},{Y}_{t-u-2\tau_{l}},...,,{Y}_{t-u-(l-1)\tau_{l}})$

Testovanie môjho estimatora či robí to čo má a či mi to sedi s JIDT

Rendered by QuickLaTeX.com

Pozorovanie:
Je to strašne pomale (pri k=2, $\tau_{k}=1$ , l=2, $\tau_{l}=1$ , sample size N=645, 155 s). Pozeral som sa na dátovú štruktúru k-d tree, ale vraj pri vysoko rozmerných dátach nie je o mnoho rýchlejší ako brute force. Tak neviem či to má vôbec zmysel implementovať.

Použité dáta:
SFI-heartRate_breathVol_bloodOx3.txt

Zdrojaky:
TE.py

September 14, 2017October 22, 2017

KSG estimator

Prvý nástrel KSG estimatora Transfer Entropy.

Parametre:

Target history embedding length=1
Target history embedding delay=1
Source history embedding length=1
Source history embedding delay=1
Delay from source to target=1
k-nearest neighbours=4

Pozorovania:
Porovnával som hodnoty TE môjho KSG algoritmu a JIDT Liziera na rovnakom datasete. Výsledky: môj=0.073745641982090104; JIDT=0.0737. Vyzerá, že celkom sedí.

Je to pomalé. Časová zložitosť je $>\mathrm{O}(N^{2})$

To Do:

Zovšeobecnit estimator na ľubovoľné hodnoty parametrov.
Pozrieť sa na optimalnejšie riešenia. (KDTree?)

Použité dáta:
SFI-heartRate_breathVol_bloodOx3.txt

Zdrojáky:
TE.py

September 6, 2017October 22, 2017

Transfer entropy

Po dlhom čase update.

Odložím si sem len referencie na literatúru, ktorú som štúdoval do teraz. Chcel som sa dostať do teórie informácie a kódovania, aby som lepšie porozumel Shannonovému chápaniu informácie a entropie. Ku tomu mi pomohla táto kniha (lepšie povedané MacKayové prednášky na základe tejto knihy):
David J. C. MacKay – Information Theory, Inference and Learning Algorithms, Cambridge University Press; Sixth Printing 2007 edition (25 Sept. 2003).

Ďalej na teóriu ohľadom Transfer Entropy a rátanie/odhadovanie tieto dve knihy:
Bossomaier, T., Barnett, L., Harré, M., Lizier, J.T. – An Introduction to Transfer Entropy, Springer International Publishing, 2016.
Michael WibralRaul VicenteJoseph T. Lizier – Directed Information Measures in Neuroscience, Springer-Verlag Berlin Heidelberg, 2014.

Na Transfer entropy pri našej úlohe sa zdá najlepšie použiť Kraskov, Stogbauer a Grassberger algoritmus (KSG). Do konca týždňa by som chcel mať napísanú prvú verziu KSG estimatora TE.

March 26, 2017October 22, 2017

NARMA a Mackey – Glass NRMSE v článkoch

Toto je skôr poznámka aby som prehľadal články kde sa odhaduje NARMA a Mackey – Glass a pozrel sa okolo akých hodôt sa hýbe NRMSE.

Boedecker- Information processing in echo state networks at the edge of chaos používam NARMU akú má Boedecker v článku a jemu sa pohybuje NRMSE okolo 0.8 čo je konzistentné s našimi pozorovaniami.

March 26, 2017October 22, 2017

NRMSE a rezervoir size

Pozeral som sa na vplyv veľkosti rezervoiru na NRMSE pri predikciach Mackey-Glass a NARMA pre 3 rôzne počty iterácií OG a ON rezervoirovej matice (0, 50, 100).

Nastavenia siete:
Počet runov = 10
Leaking rate = 1
reg=0
Počiatočný spektrálny polomer = 0.9
initLen = 100
trainLen = 2000
errorLen = 1000
Win ~ R(-0.01,0.01)
W~ N(0,1)

Ortonormalizácia

Pozn. v obrázku pre Mackey – Glass sú zle označené osi x= rezervoir size a y=NRMSE

hmm tak OG rezervoirovej matice je časovo náročná. Už pri veľkosti rezervoiru 300 to trva cca 10 min. Možno to nechám rátať cez noc.

Ortogonalizácia

Zdrojaky:

ESBrezervoirSIZE.py