Octahedra packing with simulated annealing
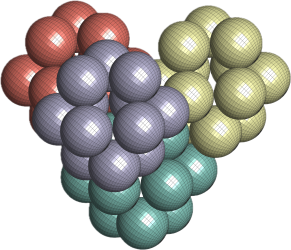
I’ve equipped the packing algorithm with simulated annealing schedule and used it to pack 8 octahedra in a unit cell. Here are some pictures from one run.
Left is the initial packing and right final packing.
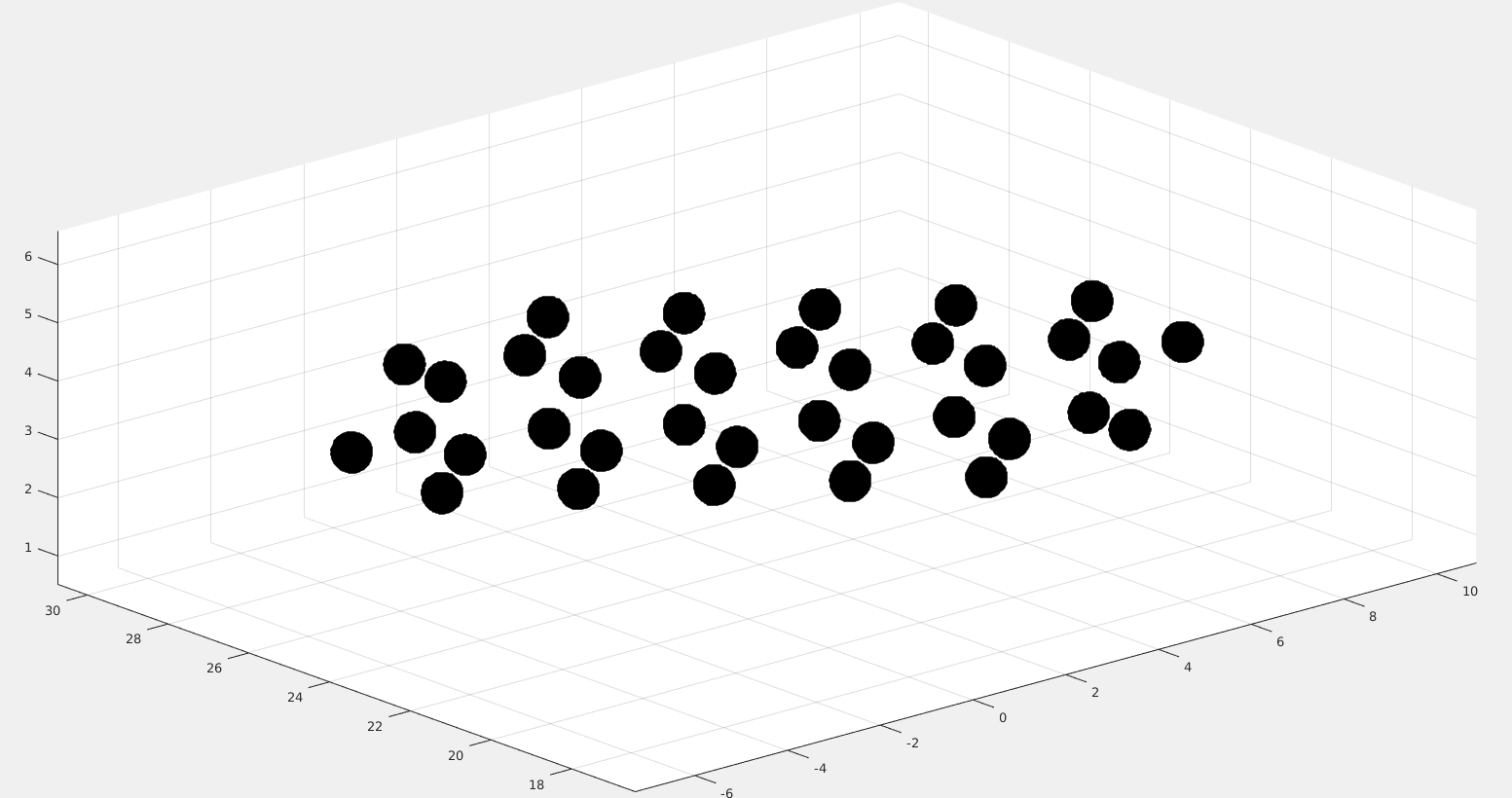
27 unit cells of the above packings.
Initial density is 0.1667. The final density is 0.9178. Optimal lattice packing density is 0.9474 (a result by Minkowski) which is hypothesised to be general optimal packing.
I ran also the algorithm without the simulated annealing with same parameters and the final density was 0.8281. Now the question is if the simulated annealing schedule is an improvement or this was achieved just by chance.
Parameter space exploration
Did some exploration of the parameter space of the packing algorithm for comparison of the C++ a Julia versions. Moved values of one parameter and fixed all others to the same values. 10 iterations for every parameter were done and collected densities of resulting packing configurations of 8 tetrahedra. The initial configuration of tetrahedra were same in all cases.
The initial density was 0.06415. The best I got from the experiments was 0.67045. Below are the visualizations of the packings.
Left initial packing of 8 tetrahedra in a unit cell and right best packing achieved.
Left 27 unit cell of the initial packing. Right 27 unit cells of the best achieved packing.
Tetrahedra packing – first experiments
It’s been a while since last post.
I’ve got hold of the polyhedra packing algorithm from Dense packings of the Platonic and Archimedean solids (thank you Yang) in C++ and rewritten it in Julia.
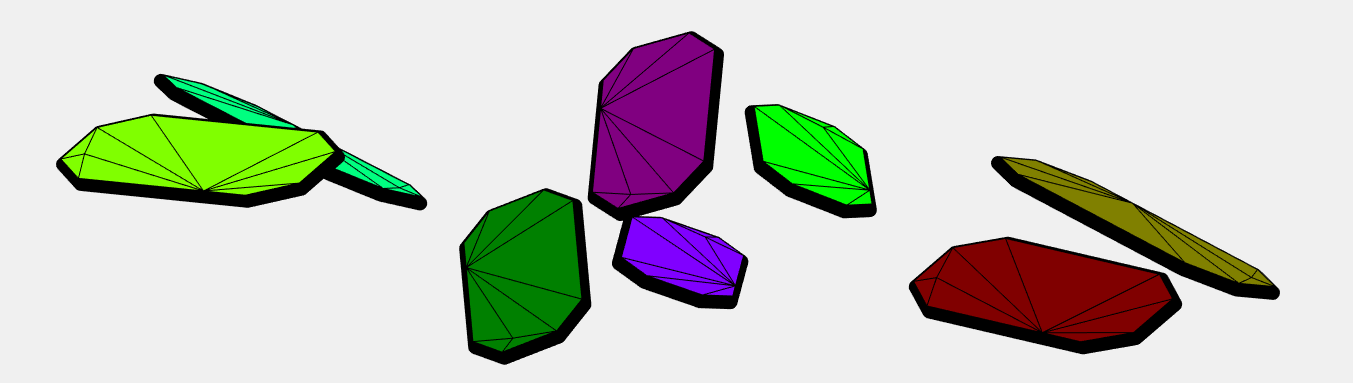
Here are the images from the first experiments of packing 8 tetrahedra in a unit cell.
Left is the initial configuration and right is the configuration after 1000 iterations.
The initial density is 0.06415 and and the density after 1000 iterations is 0.58888. For comparison the densest lattice packing of tetrahedra is 0.36735 but the densest found packing in the Nature paper is 0.82264.
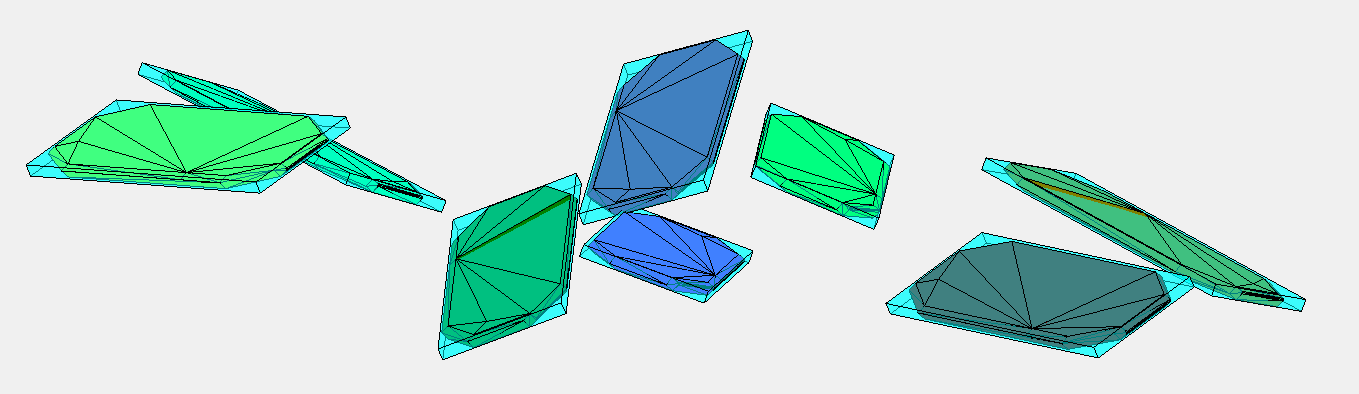
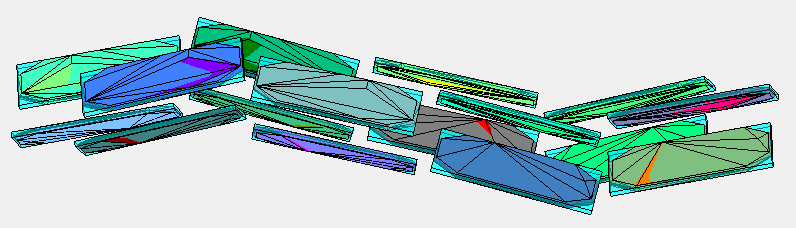
Pentacene modeling
I have taken the dataset from pentacene CSP (supplementary data from J. E. Campbell, J. Yang and G. M. DayPredicted energy–structure–function maps for the evaluation of small molecule organic semiconductors). Together 586 structures. Next I have computed minimum distance (2-norm) between pentacene molecules within every structure (0.5573). (The van der Walls radii are not good because some pentacene molecules in the structures overlap when the balls have this radius). The length of the covalent bond between two adjacent carbons is 1.3618 Angstroms. Based on this I have created a point cloud with 1108 points on a sphere around every atom of pentacene with the radius 0.5573/2.
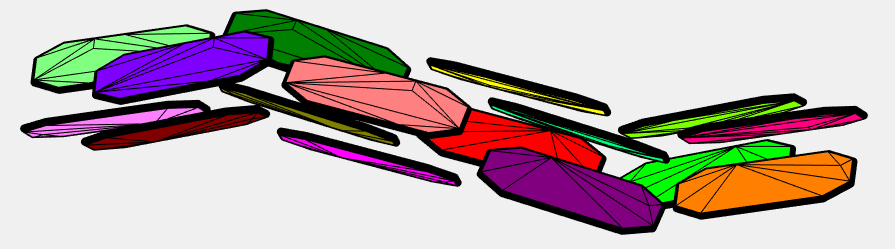
Below are the visualizations of convex hulls of the point cloud for 2 structures. On the left is the structure where the mentioned minimum is attained.
The O’Rourke’s minimum bounding box approach is not bad either, but we have to make the point could radius even smaller.
Conclusion: I think we should work with convex hulls.
Comment 1. : I discovered a stupid error I made with the minimal enclosing boxes modeling. Here it’s corrected but all the previous ones are most likely wrong.
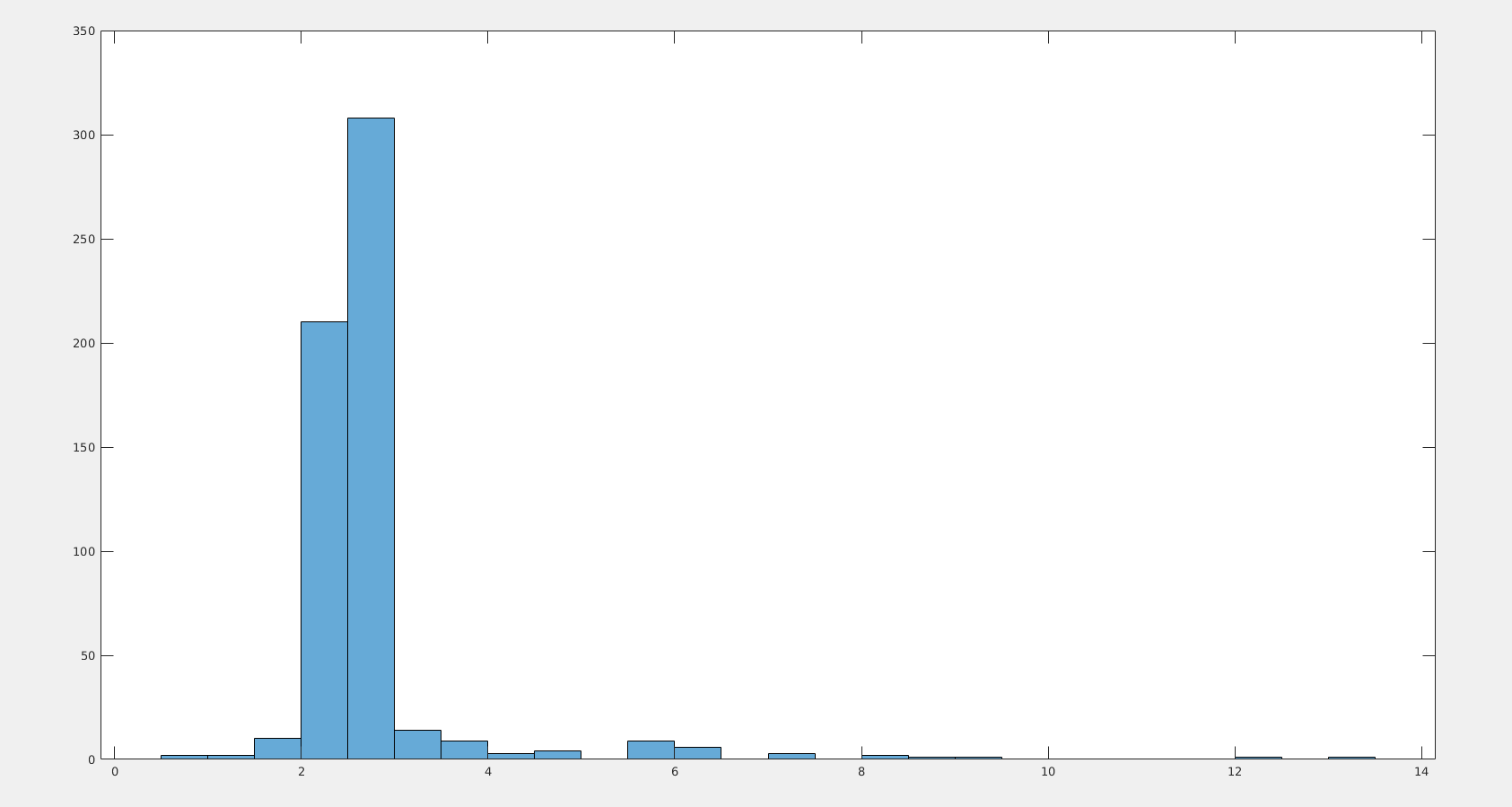
Comment 2. : the median of the minimum distances between pentacene molecules within the 586 structures is 2.6197. The histogram of the minima is below.