First simulation

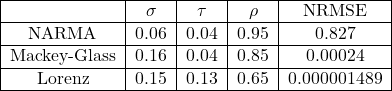
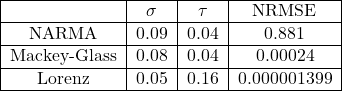
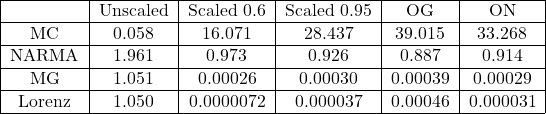
I started work with only with one enclosing box and then to continue to build upon that.

I took one enclosing box and constructed a unit cell by surrounding this central box by other boxes (as is visualized in previous post). Next I “optimized” lattice energy by Lennard-Jones potential using the centers of mass of the CC3 molecule. The central cube can by moved in 3-directions (x,y,z) but out of symmetry it’s sufficient to move only in direction in this particular case. The center of mass of CC3 is slightly off the center of mass of the small cube. That means there are 16 rotations of the central cube that can be potential minima of the energy function.

The result can by seen by below. The dots are centers of mass of CC3. The minimum was attained with no rotation of the central small box.

November 29, 2018

TDA group seminar presentation on Lattice close packings

Slides from the presentation: lattice_packings.pdf

November 29, 2018November 29, 2018

Minimal enclosing box of cage 3 (CC3)

Minimal enclosing box computed via. O’Rourk’s algorithm. The box is actually a cube:

27 of these boxes stacked together forming a unit cell:

August 16, 2018September 1, 2018

Reducing output matrix according to mean TE

The procedure for choosing output weights. First the training reservoir signals were collected and TE matrix was computed based on these signals. Next the mean TE of target unit was computed and only those units where chosen for output matrix computations which mean TE was higher then some Threshold. The threshold went from the minimum mean target TE to the maximum mean target TE in 100 steps. This was repeated 100 times. The network settings were same as in the IJCNN article for comparability reasons.

August 13, 2018August 13, 2018

Lyapunov exponent exploration revisited

This time with normalized (mean=0, variance=1) input + added a new input dataset (Multiple sinewave oscillator aka MSO)

July 18, 2018July 18, 2018

80: Sigma, Tau & Rho exploration

I have added spectral radius scaling of reservoir matrix to desired value $\rho$ along $\sigma$ and $\tau$ parameters in W $\sim$ N(0, $\sigma^2$ ) and $W^{in}$ $\sim$ Unif(- $\tau$ , $\tau$ ) to the exploration. $100$ neuron reservoir was used and $100$ instances for every pair ( $\tau$ , $\sigma$ ) were generated.

The Z values are mean NRMSE from 100 instances.

NARMA

NARMA without unscaled

Mackey – Glass

Mackey-Glass unscaled

Lorenz

Lorenz unscaled

Minimum achieved mean:
Rendered by QuickLaTeX.com

July 15, 2018July 15, 2018

79: W & Win exploration

Exploration of $\sigma$ and $\tau$ parameters in W $\sim$ N(0, $\sigma^2$ ) and $W^{in}$ $\sim$ Unif(- $\tau$ , $\tau$ ). $100$ neuron reservoir was used and $100$ instances for every pair ( $\tau$ , $\sigma$ ) were generated.