Densest P1, P-1 and P21/c packings of spheres

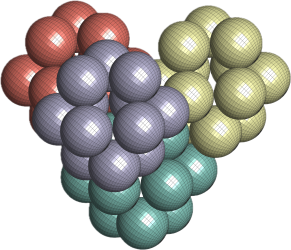
I started to work on space group packings. I applied the Entropic Trust Region Packing Algorithm (https://arxiv.org/abs/2202.11959) to search for the densest packings of the sphere in space groups P1 and P-1.

In the P1 setting, the densest packing density coincides with the general optimal packing density of spheres (https://www.jstor.org/stable/20159940). If the unit cell parameters are set to $a=b=c=2$ and $\alpha=\beta=\gamma=\frac{\pi}{3}$ with the unit cell given by

$\begin{equation*} U=\left[\begin{array}{ccc} a\sin(\beta)\sqrt{1-\left(\frac{\cos(\alpha)cos(\beta) - cos(\gamma)}{\sin(\alpha)\sin(\beta)}\right)^2} & 0 & 0 \\ -a\frac{\cos(\alpha)cos(\beta) - cos(\gamma)}{\sin(\alpha)} & b\sin(\alpha) & 0 \\ a\cos(\beta) & b\cos(\alpha) & c \end{array}\right] \end{equation*}$

then the determinant of $U$ equals to $\det(U)=4\sqrt{2}$ and combined with the volume of the unit sphere $\text{vol}(S)=\frac{4}{3}\pi$ gives the optimal packing density of spheres $\rho(S_{P1})=\frac{\text{vol}(S)}{\det(U)}=\frac{\pi}{\sqrt{18}}\approx 0.74048$ . See a visualization of this configuration below.

There are a few interesting things about this. First, for some reason, I could find this configuration reported anywhere. Second, it is conjectured that the densest packings of centrally symmetric polyhedra are P1 packings (https://journals.aps.org/pre/abstract/10.1103/PhysRevE.80.041104). It might be that this conjecture can be extended to a larger class of centrally symmetric convex sets, similar to the 2D setting where the densest packing of centrally symmetric convex sets is a lattice packing (https://link.springer.com/article/10.1007/BF02392671).

In the P-1 setting the situation is similar. If the unit cell parameters are set to $a=c=2$ , $b=2\sqrt{2}$ and $\alpha=\beta=\gamma=\frac{\pi}{2}$ , then the determinant of the unit cell equals to $\det(U)=8\sqrt{2}$ and again we get the optimal packing density of spheres $\rho(S_{P-1})=\frac{2\text{vol}(S)}{\det(U)}=\frac{\pi}{\sqrt{18}}$ . See the visualization of this configuration below.

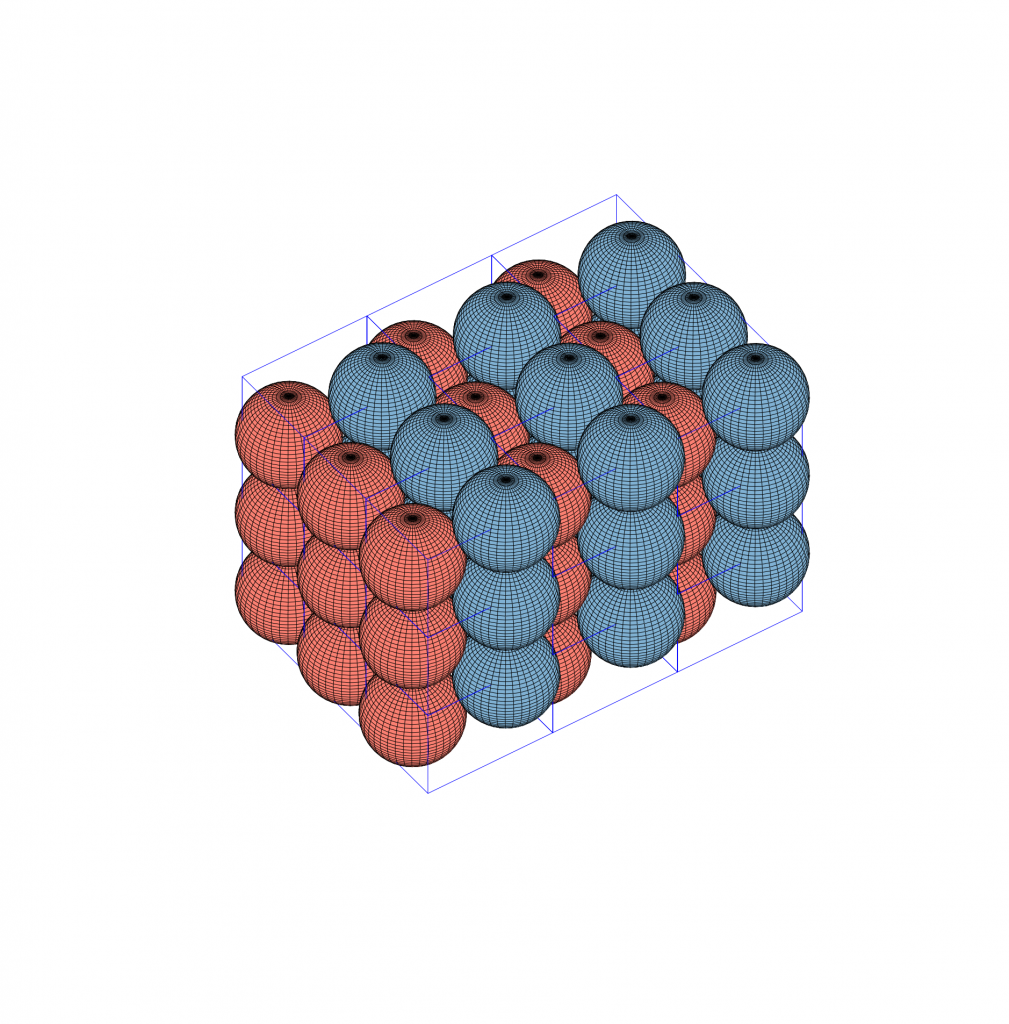
Here again, I couldn’t find this configuration of spheres reported anywhere. Another interesting thing is that the situation resembles the 2D setting, where the densest P1 and P2 configurations of a disc have the same packing density (https://journals.aps.org/pre/abstract/10.1103/PhysRevE.106.054603). The P-1 space group can be considered as an equivalent of the P2 plane group since the point group symmetries are given via inversion through the centre of the unit cell. It might be that centrally symmetric polyhedra attain their optimal packings also in the P-1 space group. Moreover, it is conjectured that for convex 2D sets, the P2 configurations are optimal (https://link.springer.com/article/10.1007/s00454-016-9792-4). I am wondering for which other convex 3D sets is the P-1 packing configuration optimal.

With the P21/c space group, the symmetries of the densest sphere packing continue. If the unit cell parameters are set to $a=2\sqrt{2}$ , $b=4$ , $c=2$ and $\alpha=\beta=\gamma=\frac{\pi}{2}$ , then the determinant of the unit cell equals to $\det(U)=16\sqrt{2}$ and again we get the optimal packing density of spheres $\rho(S_{P21/c})=\frac{4\text{vol}(S)}{\det(U)}=\frac{\pi}{\sqrt{18}}$ . See the visualization of this configuration below.

What is interesting is that the P21/c and P-1 space groups are the most frequent space groups found in the Cambridge Structural Database amounting to 59.3% of structures (https://www.ccdc.cam.ac.uk/support-and-resources/ccdcresources/f0dbc77b8b6041b8be63ff490bad33d6.pdf). I wonder if there is a relationship between densest space group packing of a sphere and the frequencies space groups occurring in CSD.