I needed a way to calculate the packing densities of structures modeled using the van der Waals sphere model, generated through CSP and DFT computations. Specifically, for periodic configurations, this comes down to computing:: ![]() . Here,
. Here, ![]() represents the volume of the unit cell
represents the volume of the unit cell ![]() , and
, and ![]() is the volume of the subset of
is the volume of the subset of ![]() occupied by the van der Waals spheres denoted as
occupied by the van der Waals spheres denoted as ![]() .
.
Calculating the volume of ![]() is is straightforward; it’s simply the determinant of the unit cell’s generators:
is is straightforward; it’s simply the determinant of the unit cell’s generators: ![]() . However, analytically computing the volume of
. However, analytically computing the volume of ![]() involves solving numerous intricate integrals of intersections of spheres with various radii, making it cumbersome.
involves solving numerous intricate integrals of intersections of spheres with various radii, making it cumbersome.
Let’s try to do this the Monte-Carlo way, instead. The volume of ![]() can be expressed as an integral over the unit cell
can be expressed as an integral over the unit cell ![]() , i.e.
, i.e.
![]()
Here, ![]() is the natural volume form on
is the natural volume form on ![]() . Since this integral is zero everywhere except in the unit cell, it can be redefined as an integral of the indicator function over the unit cell:
. Since this integral is zero everywhere except in the unit cell, it can be redefined as an integral of the indicator function over the unit cell:
![]()
By changing coordinates to an integral over the unit cube ![]() , we get:
, we get:
![]()
Plugging this into the density equation yields:
![]()
Considering ![]() as a uniform random vector on the unit cube, this integral represents the expected value of the indicator function with respect to the
as a uniform random vector on the unit cube, this integral represents the expected value of the indicator function with respect to the ![]() -variate uniform distribution. This, in turn, equals the probability of
-variate uniform distribution. This, in turn, equals the probability of ![]() lying in the collection of the van der Waals spheres
lying in the collection of the van der Waals spheres ![]() , scaled by the inverse of the unit cell:
, scaled by the inverse of the unit cell:
![]()
This means that the crystal’s density can be estimated by sampling ![]() , counting how many fall inside
, counting how many fall inside ![]() , and dividing by
, and dividing by ![]() :
:
![]()
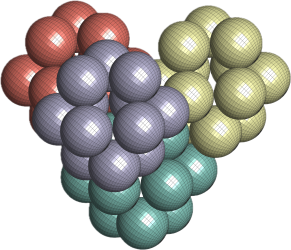
Now, say I want to determine the density of this ![]() anthracene structure
anthracene structure
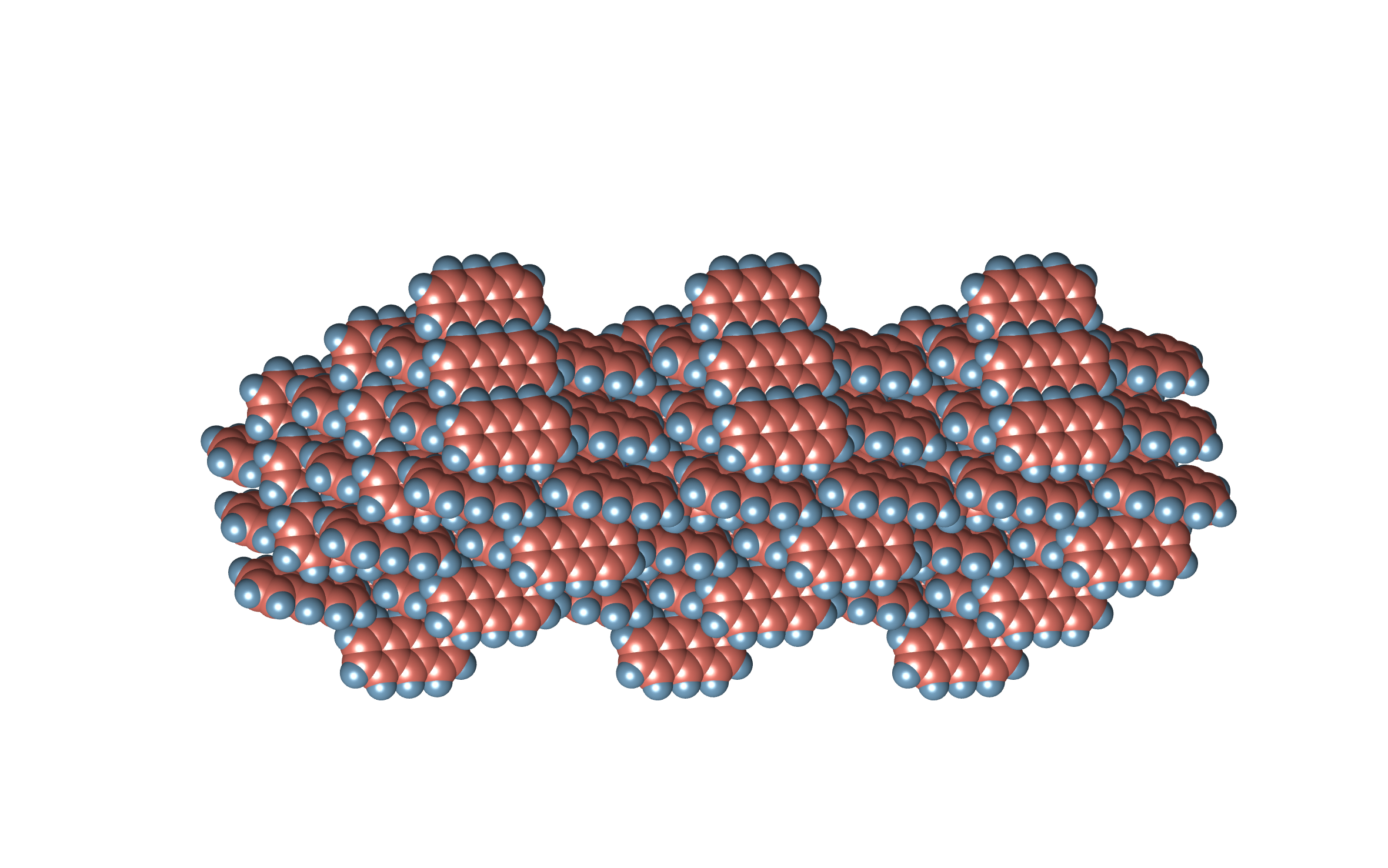
Equivalently, I can sample uniformly from the parallelepiped defined by the unit cell, e.g. ![]() realisations,
realisations,

and count how many fall inside at least one of the van der Waals spheres

which is ![]() . Therefore, the density estimate is
. Therefore, the density estimate is ![]() .
.
But how accurate is this estimate? Or even better, how large does ![]() need to be so that
need to be so that ![]() , where
, where ![]() is some constant?
is some constant?
To answer this, consider each ![]() as a Bernoulli trial. Then
as a Bernoulli trial. Then ![]() is a binomially distributed random variable with the expected value
is a binomially distributed random variable with the expected value ![]() and variance
and variance ![]() . According to the central limit theorem, the random variable
. According to the central limit theorem, the random variable ![]() converges in distribution to a normally distributed random variable with a mean of
converges in distribution to a normally distributed random variable with a mean of ![]() and a variance of
and a variance of ![]() . Therefore, I can request
. Therefore, I can request ![]() being in the interval
being in the interval ![]() , and I want the size of this interval to be less than some constant with probability
, and I want the size of this interval to be less than some constant with probability ![]() :
:
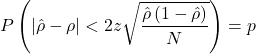
where ![]() is the
is the ![]() quantile of the standard normal distribution.
quantile of the standard normal distribution.
For the ![]() anthracene structure mentioned earlier, to achieve
anthracene structure mentioned earlier, to achieve ![]() with probability
with probability ![]() , I need
, I need ![]() . The density estimate in this case is then:
. The density estimate in this case is then:
![]()
As a point of comparison, CCDC’s Mercury reports the packing coefficient of this structure as ![]() .
Closing note: This method could also be used to quantify uncertainty about the true packing during ETRPA‘s optimization run in the tradition of Sequential analysis.
.
Closing note: This method could also be used to quantify uncertainty about the true packing during ETRPA‘s optimization run in the tradition of Sequential analysis.